
如图,某村庄计划把河中的水引到水池M中,怎样开的渠最短,为什么?(保留作图痕迹,不写作法和证明)
理由是: .

科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
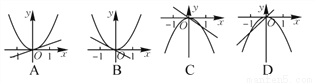
A. (A) B. (B) C. (C) D. (D)
C 【解析】试题分析:当a>0时,y=ax过一三象限,y=ax2在一二象限,且当ax=ax2 时,可判断两函数有两个交点,所以A、B错,当a<0时,y=ax过二四象限,y=ax2在三四象限,两函数的交点坐标为(0,0)(1,a),故选C.查看答案和解析>>
科目:初中数学 来源:湖南省耒阳市冠湘学校2018届九年级上学期第二次段考(期中)考试数学试卷 题型:解答题
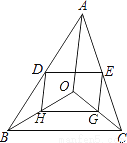
如图,在△ABC中,D、E分别是边AB、AC的中点,O是三角形内部一点,连接OB、OC,G、H分别是OC、OB的中点,试说明四边形DEGH是平行四边形.
查看答案和解析>>
科目:初中数学 来源:湖南省耒阳市冠湘学校2018届九年级上学期第二次段考(期中)考试数学试卷 题型:单选题
关于x的一元二次方程(a﹣1)x2 +x + a2﹣1=0的一个根是0,则a的值为( )
A. ﹣1 B. 1 C. 1或﹣1 D. 0.5
A 【解析】试题分析:由题意可知,将x=0代入方程得,解得 又因为即 所以a=-1 故选A查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
按下面的方法折纸,然后回答问题:

(1)∠1与∠AEC有何关系?
(2)∠1,∠3有何关系?
(3)∠2是多少度的角?请说明理由.
(1)互补;(2)互余;(3)90° 【解析】试题分析:(1)由折叠易得∠2是平角的一半; (2)∠1、∠2、∠3组成一个平角,∠2是90°,那么∠1与∠3互余; (3)∠1与∠AEC,∠3与∠BEF都组成一个平角,是互补. 试题解析:(1)∠2是90°的角。 过点E作出AB、EC的折痕,设BE、CE与EG重合,由折纸可知: ∠1=∠AEG,∠3=∠FEG, ...查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
已知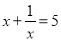 ,那么
,那么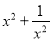 =_______。
=_______。
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
计算: 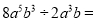 ______________。
______________。
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.5应用一元一次方程-“希望工程”义演 同步练习 题型:填空题
某次数学测验共有20题,每题答对得5分,不答得0分,答错得﹣2分.若小丽这次测验得分是质数,则小丽这次最多答对______题.
17 【解析】最多答对17道。原因如下: 如果答对19道,若另一道不答,是95分,不符合题意;若另一道答错,得93分,也不符合题意。 如果答对17道,若另三道不答,是85分,不符合题意;若另两道不答,一道答错,得83分,符合题意。 故答案为:17.查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为________.
30° 【解析】试题分析:此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可. 由题意得:α=2β,α=110°,则β=55°, 180°-110°-55°=15°, 故答案为:15°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com