练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

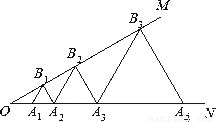
    如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1=2，则△A5B5A6的边长为( )

    A. 8 B. 16 C. 24 D. 32

    B 【解析】如图所示： ∵△A1B1A2是等边三角形， ∴A1B1=A2B1，∠3=∠4=∠12=60°， ∴∠2=120°， ∵∠MON=30°， ∴∠1=180°﹣120°﹣30°=30°， 又∵∠3=60°， ∴∠5=180°﹣60°﹣30°=90°， ∵∠MON=∠1=30°， ∴OA1=A1B1=1， ∴A2B1=1， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：单选题

    有理数﹣1的绝对值是（　　）

    A. 1 B. ﹣1 C. ±1 D. 2

    A 【解析】根据绝对值的意义，-1的绝对值是1. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：填空题

    挂钟分针的长10cm，经过45分钟，它的针尖转过的弧长是 cm.

    ． 【解析】 试题分析：分针经过60分钟，转过360°，经过45分钟转过270°， 则分针的针尖转过的弧长是． 故答案是．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    如图，在△ABC中，AB=AC，∠A=36°，DE是AC的垂直平分线．

    （1）求证：△BCD是等腰三角形；

    （2）△BCD的周长是a，BC=b，求△ACD的周长（用含a，b的代数式表示）

    （1）见解析；（2）a﹣b+b+b=a+b． 【解析】试题分析:（1）先由AB=AC，∠A=36°，可求∠B=∠ACB==72°，然后由DE是AC的垂直平分线，可得AD=DC，进而可得∠ACD=∠A=36°，然后根据外角的性质可求：∠CDB=∠ACD+∠A=72°，根据等角对等边可得：CD=CB，进而可证△BCD是等腰三角形； （2）由（1）知：AD=CD=CB=b，由△BCD的周长是...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    如图，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C，若PC=6，则PD= ．

    3． 【解析】 试题分析：过点P作PE⊥OA于E，根据角平分线定义可得∠AOP=∠BOP=15°，再由两直线平行，内错角相等可得∠BOP=∠OPC=15°，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=30°，再根据直角三角形30°角所对的直角边等于斜边的一半解答． 【解析】 如图，过点P作PE⊥OA于E， ∵∠AOB=30°，OP平分∠AOB， ...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    一个多边形每个外角都等于36°，则这个多边形是几边形（ ）

    A．7 B．8 C．9 D．10

    D 【解析】 试题分析：多边形的外角和是360°，又有多边形的每个外角都等于36°，所以可以求出多边形外角的个数，进而得到多边形的边数． 【解析】 这个多边形的边数是：=10．故答案是D．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

    在矩形ABCD中，AD=3，CD=4，点E在CD上，且DE=1．

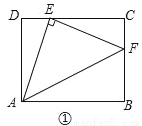
    （1）感知：如图①，连接AE，过点E作EF丄AE，交BC于点F，连接AE，易证：△ADE≌△ECF（不需要证明）；

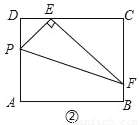
    （2）探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE和△ECF相似；

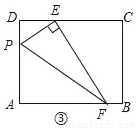
    （3）应用：如图③，若EF交AB于点F，EF丄PE，其他条件不变，且△PEF的面积是6，则AP的长为_____．

    3﹣ 【解析】试题分析：感知：先利用矩形性质得：∠D=∠C=90°，再利用同角的余角相等得：∠DAE=∠FEC，根据已知边的长度计算出AD=CE=3，则由ASA证得：△ADE≌△ECF； 探究：利用两角相等证明△PDE∽△ECF； 应用：作辅助线，构建如图②一样的相似三角形，利用探究得：△PDE∽△EGF，则 =，所以 =，再利用△PEF的面积是6，列式可得：PE•EF=12，两...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    不等式组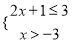中的两个不等式的解集在同一个数轴上表示正确的是（　　）

    A. 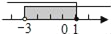B.

    C. D.

    A 【解析】 解①得， . ∴不等式组得解集是 . 故选A.

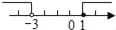
    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：填空题

    如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA于点E，若∠B=30°，则线段AE的长为 ．

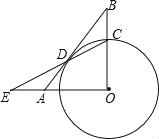
    【解析】 试题分析：要求AE的长，只要求出OA和OE的长即可，要求OA的长可以根据∠B=30°和OB的长求得，OE可以根据∠OCE和OC的长求得．连接OD，如图所示， 由已知可得，∠BOA=90°，OD=OC=3，∠B=30°，∠ODB=90°，∴BO=2OD=6，∠BOD=60°， ∴∠ODC=∠OCD=60°，AO=BOtan30°=6×=2，∵∠COE=90°，OC=3， ...

    查看答案和解析>>

    同步练习册答案