
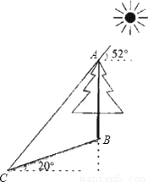
如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
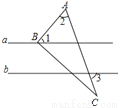
如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
五边形的内角和等于____度,十边形的对角线有__条.
540 35 【解析】【解析】 五边形的内角和=(5-2)×180°=540°,十边形的对角线条数=10×(10-3)÷2=35.故答案为:540;35.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
用长为6m的铝合金型材做一个形状如图所示的矩形窗框,要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成( )

A. 1.5m,1m B. 1m,0.5m C. 2m,1m D. 2m,0.5m
A 【解析】试题分析:设长为x,则宽为,S=,即S=, 要使做成的窗框的透光面积最大,则x=,于是宽为=1m, 所以要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成1.5m,1m,故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图刻画( )
A. 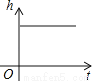 B.
B. 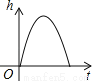 C.
C. 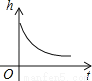 D.
D. 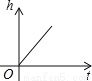
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:填空题
已知一个正六边形的边心距为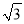 ,则它的半径为______ .
,则它的半径为______ .
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
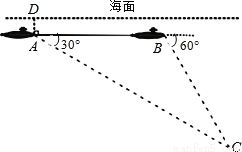
A. 2000米 B. 4000米 C. 2000米 D. (2000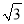 +500)米
+500)米
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:填空题
某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x个,根据题意可列方程为______.
20x=15(x+4)-10. 【解析】根据等量关系:实际15天完成的数量比计划20天完成的数量多10个,设原计划每天生产x个,原计划20天生产数量为:20x,实际15天生产的数量为:15(x+4),根据题意可列出方程为: 20x=15(x+4)-10,故答案为: 20x=15(x+4)-10.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:单选题
如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,则∠BAE的度数为( )
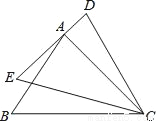
A. 15° B. 55° C. 65° D. 75°
A 【解析】试题解析:∵△ABC绕点C按顺时针旋转15°到△DEC, ∴∠ACD=15°,∠BAC=∠D, ∵∠EAC=∠D+∠ACD, 即∠BAE+∠BAC=∠D+∠ACD, ∴∠BAE=∠ACD=15°. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com