
若-4≤x≤3,化简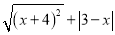 的结果为( )
的结果为( )
A. 2x+1 B. -2x-1 C. 1 D. 7
D 【解析】已知-4≤x≤3,可得x+4≥0,3-x≥0,根据非负数的性质可得,原式=x+4+3-x=7,故选D. 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
在下列图形中,线段PQ的长度表示点P到直线L的距离的是( )
A.  B.
B. 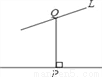 C.
C. 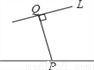 D.
D. 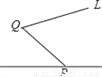
查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:填空题
某种药品经过两次降价由原来的每盒 12.5 元降到每盒 8 元,如果 2 次降价的百分率相同,设每次降价的百分率为 x,可列出的方程为_____.
12.5(1-x)2=8 【解析】【解析】 根据题意得:12.5(1﹣x)2=8.故答案为:12.5(1﹣x)2=8.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
已知a,b为一个等腰三角形的两条边长,并满足b=2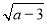 +
+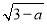 +5,求此等腰三角形的周长.
+5,求此等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.

以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
A. ③→②→①→④ B. ③→④→①→②
C. ①→②→④→③ D. ①→④→③→②
B 【解析】根据菱形四条边相等的性质可得AB=AD,OB=OD,根据等腰三角形三线合一的性质可得AO⊥BD,即可得AC⊥BD,所以正确的顺序为③→④→①→②,故选B.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
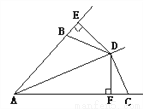
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题

查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.


查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.

A. 1 B. 2 C. 3 D. 4
C 【解析】∵BE⊥AC,CF⊥AB, ∴∠AEB=∠AFC=∠CED=∠DFB=90°. 在△ABE和△ACF中, , ∴△ABE≌△ACF(AAS), ∴AE=AF. ∵AC=AB, ∴CE=BF. 在△CDE和△BDF中, , ∴△CDE≌△BDF(AAS) ∴DE=DF. ∵BE⊥AC于E,CF⊥AB, ∴...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com