练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在□x2□2x□1的空格中,任意填上“＋” ,“－”,共有_____种不同的代数式,其中能构成完全平方式的有______种.

    8 4 【解析】【解析】 共有8种具体如下：x2±2x+1；x2±2x﹣1；﹣x2±2x+1；﹣x2±2x﹣1． 其中x2±2x+1、﹣x2±2x﹣1是完全平方式． 故答案为：8，4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 21.2.1配方法（1）练习 题型：解答题

    已知方程(x－1)2＝k2＋2的一个根是x＝3，求k的值和方程的另一个根．

    k＝±，-1. 【解析】试题分析： 先把x=3代入到原方程中，求得k的值，再把k的值代回到原方程中求另一个根. 试题解析： 把x＝3代入方程得k的值为±，再把k＝±代入方程得另一个根为－1.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（2）测试 题型：单选题

    在图形旋转中，下列说法错误的是（　　）

    A. 图形上的每一点到旋转中心的距离相等 B. 图形上的每一点转动的角度相同

    C. 图形上可能存在不动点 D. 图形上任意两点的连线与其对应两点的连线相等

    A 【解析】A选项,在图形旋转中,根据旋转的性质,图形上对应点到旋转中心的距离相等,故A选项错误, B选项,图形上的每一点转动的角度都等于旋转角,故B选项正确, C选项,图形上一点为旋转中心,则这个点不动, 故C选项正确, D选项,旋转前后两个图形全等,则图形上任意两点的连线与其对应两点的连线相等, 故D选项正确, 故选A.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.4弧长和扇形面积（2）练习 题型：填空题

    圆锥的底面积为25π，母线长为13 cm，这个圆锥的底面圆的半径为________ cm，高为________ cm，侧面积为________ cm2.

    5；12； 65π. 【解析】设底面半径是r,高是h ∵s= ， 25π= ， r=5. h=, 底面周长是10， .

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：解答题

    某鱼塘捕到100条鱼,称得总重为150千克,这些鱼大小差不多, 做好标记后放回鱼塘,在它们混入鱼群后又捕到102条大小差不多的同种鱼,称得总重仍为150千克,其中有2条带有标记的鱼.（1）鱼塘中这种鱼大约有多少条? （2）估计这个鱼塘可产这种鱼多少千克?

    （1）5100（2）7573.5千克 【解析】试题分析：由题意可知：本题是估算题，可以设这种鱼有x条，由可能事件的概率公式知102：2=x：100；再用乘以每条质量即得鱼的总质量．每条鱼的质量是千克． 试题解析：【解析】 （1）设鱼塘中一共有鱼x条，102：2=x：100，所以x= =5100； （2）5100×≈7573.5（千克） 答：鱼塘中这种鱼大约有5100条，这...

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：填空题

    如图，每一个标有数字的方块均是可以翻动的木牌，其中只有两块木牌的背面贴有中奖标志，则随机翻动一块木牌中奖的概率为_______.

    【解析】【解析】 P（中奖）==．故答案为： ．

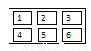
    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：单选题

    在一个暗箱里放有a个除颜色外其它完全相同的球，这a个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a大约是（     ）．

    A. 12 B. 9 C. 4 D. 3

    A 【解析】摸到红球的频率稳定在25%，即=25%，即可即解得a的值 【解析】 ∵摸到红球的频率稳定在25%，∴=25%，解得：a=12． 故本题选A.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（2）测试 题型：填空题

    与抛物线y=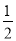x2的形状和开口方向相同，顶点为（3，1）的二次函数解析式为______．

    y=（x﹣3）2+1 【解析】试题分析：利用顶点式即可求解. 【解析】 设抛物线解析式为y=a（x﹣3）2+1， 因为抛物线y=a（x﹣3）2+1与抛物线y=x2的形状和开口方向相同， 所以a=， 所以所求抛物线解析式为y=（x﹣3）2+1． 故答案为：y=（x﹣3）2+1．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

    如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.

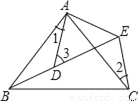
    55° 【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可． 【解析】 ∵∠BAC=∠DAE， ∴∠BAC﹣∠DAC=∠DAE﹣∠DAC， ∴∠1=∠EAC， 在△BAD和△EAC中， AB=AC，∠BAD=∠EAC， ∴△BAD≌△EAC（SAS）， ∴∠2=∠ABD=30°， ∵...

    查看答案和解析>>

    同步练习册答案