
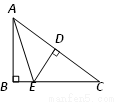
如图,在Rt△ABC中,AB⊥BC,DE⊥AC,AD=CD,∠BAE=20°,则∠C=___________.
【答案】35°
【解析】∵DE⊥AC,AD=CD,
∴AE=CE,
∴∠C=∠EAD,
∵AB⊥BC,
∴∠B=90°,
∴∠C+∠EAD+∠BAE=90°,
∵∠ABE=20°,
∴2∠C=70°,∠C=35°.
【题型】填空题
【结束】
17
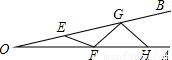
如图,∠AOB是一角度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FG、GH…,且OE=EF=FG=GH…,在OA、OB足够长的情况下,最多能添加这样的钢管的根数为 _________.
科目:初中数学 来源:安徽省合肥市2017-18学年度第一学期 第三次月考 七年级数学试卷 题型:单选题
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
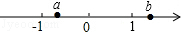
A. a+b<0 B. a﹣b<0 C. a•b>0 D. 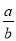 >0
>0
查看答案和解析>>
科目:初中数学 来源:江苏省等六校2018届九年级12月月考数学试卷 题型:填空题
如图,已知A(6,0),B(4,3)为平面直角坐标系内两点,以点B圆心的⊙B经过原点O,BC⊥x轴于点C,点D为⊙B上一动点,E为AD的中点,则线段CE长度的最大值为_______.

查看答案和解析>>
科目:初中数学 来源:江苏省等六校2018届九年级12月月考数学试卷 题型:单选题
一元二次方程x2=2x的解为( )
A. x=0 B. x=2 C. x=0或x=2 D. x=0且x=2
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级12月月考数学试卷 题型:解答题
解方程: 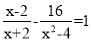 .
.
【答案】原方程无解.
【解析】试题分析:按照解分式方程的步骤解方程即可.
试题解析: 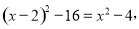
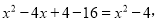
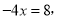
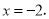
经检验:x=-2是增根.
原方程无解.
点睛:注意:分式方程必须进行检验.
【题型】解答题
【结束】
22
(2017山东省菏泽市)先化简,再求值: 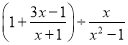 ,其中x是不等式组
,其中x是不等式组 的整数解.
的整数解.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级12月月考数学试卷 题型:填空题
若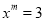 ,
, 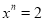 ,则
,则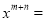 ___________。
___________。
【答案】6
【解析】∵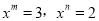 ,
,
∴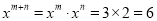 .
.
【题型】填空题
【结束】
12
如果(x-2)(x+3)=x2+px+q,那么p+q的值为________.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级12月月考数学试卷 题型:单选题
把分式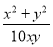 中的
中的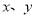 都扩大为原来的5倍,分式的值( )
都扩大为原来的5倍,分式的值( )
A. 不变 B. 扩大5倍 C. 缩小为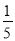 D. 扩大25倍
D. 扩大25倍
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第四教育联盟2018届九年级上学期第二次质量检测(12月月考)数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
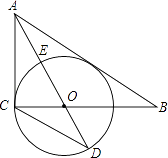
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=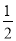 ,求
,求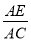 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】(1)证明见解析(2)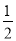 (3)
(3)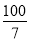
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得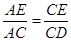 = tanD=
= tanD=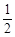 ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得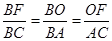 ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F
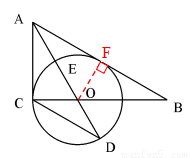
∵AO是∠BAC的角平分线,∠ACB=90º
∴OC=OF
∴AB是⊙O的切线
(2)连接CE
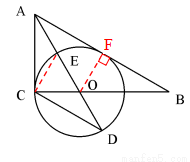
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴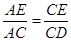 = tanD=
= tanD=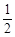
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)²="(2x)" ²+3² ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得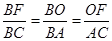 ,
,
设BO=y BF=z
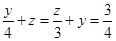
即4z=9+3y,4y=12+3z
解得z=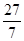 y=
y=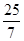
∴AB=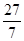 +4=
+4=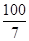
考点:圆的综合题.
【题型】解答题
【结束】
24
一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com