
二次函数y=x2﹣2x+3的图象的顶点坐标是( )
A. (1,2) B. (1,6) C. (﹣1,6) D. (﹣1,2)
A 【解析】试题分析:y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,所以抛物线y=x2﹣2x+3的顶点坐标是(1,2).故选A.科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:解答题
解不等式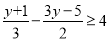 ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
如图,在4×4的方格中(共有16个小方格),每个小方格都是边长为1的正方形,O,A,B分别是小正方形的顶点,则扇形OAB的弧长等于( )
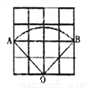
A. 2π B. 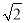 π C. 2
π C. 2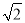 π D.
π D. 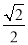 π
π
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为_____.
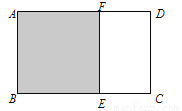
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
如图1,在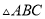 中,
中, 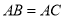 ,
, 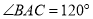 .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
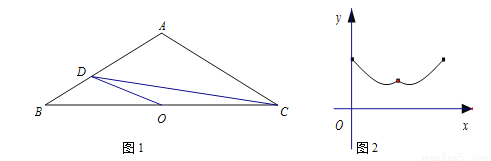
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为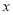 ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
A. 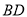 B.
B. 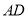 C.
C. 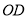 D.
D. 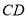
查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:解答题
10袋小麦以每袋150千克为准,超过的千克数记为正数,不足的千克数记为负数,分别记为:﹣6,﹣3,0,﹣3,+7,+3,+4,﹣3,﹣2,+1.
(1)与标准重量相比较,10袋小麦总计超过或不足多少千克?
(2)10袋小麦中哪一个记数重量最接近标准重量?
(3)每袋小麦的平均重量是多少千克?
(1)不足2千克;(2)第三个;(3)149.8千克. 【解析】试题分析:(1)先求-﹣6,﹣3,0,﹣3,+7,+3,+4,﹣3,﹣2,+1的和,是正数,则超过,是负数,则不足; (2)根据绝对值即可进行判断,绝对值最小的接近标准重量; (3)求得10袋小麦以每袋150千克为准时的总量,再加上(1)中的结果,然后用总量除以10,即可求得每袋小麦的平均重量. 试题解析:(1...查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3h,若船在静水中速度为26km/h,水流速度为2km/h,则A港和B港相距_____km.
504 【解析】试题分析:设轮船从A港顺流行驶到B港所需的时间为t,则从B港逆流返回A港的时间为t+3,因船速为26千米/小时,水速为2千米/时,则顺流速度为26+2=28km/h,逆流速度为26-2=24km/h,则有28t=24(t+3),解得t=18,所以A港和B港的距离为28×18=504km.查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(2,7) ,直线l经过A点且平行于x
轴,直线l上的动点C从A点出发以每秒4个单位的速度沿直线l运动.若在x轴上有两点D、E,
连接DB、OB,连接EC、OC,满足DB=OB,EC=OC,设点C运动时间t秒,
(1) 如图1,若动点C从A点出发向左运动,当t=1秒时,
①求线段BC的长和点E的坐标;
②求此时DE与AC的数量关系?
(2)探究:动点C在直线l运动,无论t取何值,是否都存在上述(1)②中的数量关系? 若存在,请证明;若不存在,请说明理由.
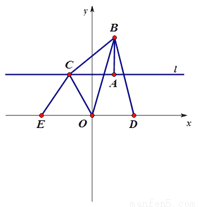
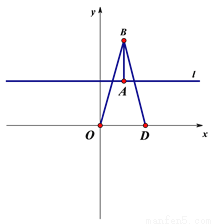
图1 图2
(1) ①BC=5, E(-4,0)②DE=2AC (2)存在,证明见解析 【解析】试题分析:(1)①根据题意可知AC=4,AB=3,由勾股定理即可得BC的长,再根据EC=OC以及点C的坐标即可得点E的坐标; ②由点B的坐标以及DB=OB即可得点D的坐标,从而得到DE的长,从而可得; (2)由题意可知AC=4t,C(2-4t,4),从而可得E(4-8t,0),由D(4,0)可得D...查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________
80° 【解析】试题解析:180°-50°×2 =180°-100° =80°. 故这个三角形的顶角的度数是80°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com