
定义运算:a?b=a(1﹣b).若a,b是方程x2﹣x+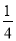 m=0(m<0)的两根,则b?b﹣a?a的值为( )
m=0(m<0)的两根,则b?b﹣a?a的值为( )
A. 0 B. 1 C. 2 D. 与m有关
A 【解析】由根与系数的关系可找出a+b=1,ab=m,根据新运算,找出b?b﹣a?a=b(1﹣b)﹣a(1﹣a),将其中的1替换成a+b,即可得出结论. 【解析】 ∵a,b是方程x2﹣x+m=0(m<0)的两根, ∴a+b=1,ab=m. ∴b?b﹣a?a=b(1﹣b)﹣a(1﹣a)=b(a+b﹣b)﹣a(a+b﹣a)=ab﹣ab=0. 故选A. “点睛”本题考查了根与系数的关... 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:四川省江县初中2016年秋季七年级期末考试 题型:单选题
如图一个正方形和一个长方形有一部分重叠在一起,重叠部分是边长为3的正方形,则未重叠部分的面积是( )
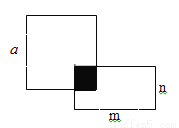
A. 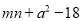 B.
B. 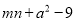 C.
C. 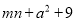 D.
D. 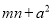
查看答案和解析>>
科目:初中数学 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:填空题
已知x1和x2分别为方程x2+x﹣2=0的两个实数根,那么x1+x2=_______;x1•x2=_______.
-1, -2 【解析】∵方程x²+x?2=0中a=1,b=1,c=?2, ∴+==?=?1, == =?2, 故答案为:?1;?2.查看答案和解析>>
科目:初中数学 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
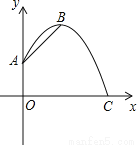
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
查看答案和解析>>
科目:初中数学 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:填空题
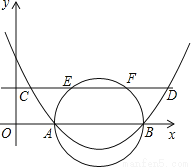
如图,抛物线过点 A(2,0)、B(6,0)、C(1, 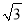 ),平行于x轴的直线CD交抛物线于C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是_____________.
),平行于x轴的直线CD交抛物线于C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是_____________.
查看答案和解析>>
科目:初中数学 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:单选题
抛物线y=ax2-2ax-3的对称轴为( )
A. 直线x=2 B. 直线x=-2 C. 直线x=1 D. 直线x=-1
C 【解析】根据抛物线对称轴公式可知抛物线y=ax2-2ax-3的对称轴为:直线x=- =1, 故选C.查看答案和解析>>
科目:初中数学 来源:北京市丰台区2017-2018学年七年级上学期期末考试数学试卷(WORD版) 题型:解答题
如图,已知直线AB及直线AB外一点P,按下列要求完成画图和解答:(1)连接PA,PB,用量角器画出∠APB的平分线PC,交AB于点C;
(2)过点P作PD⊥AB于点D;
(3)用刻度尺取AB中点E,连接PE;
(4)根据图形回答:点P到直线AB的距离是线段 的长度.
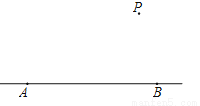
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2017-2018学年七年级上学期期末考试数学试卷(WORD版) 题型:单选题
小华家要进行室内装修,设计师提供了如下四种图案的地砖,爸爸希望灰白两种颜色的地砖面积比例大致相同,那么下面最符合要求的是( )
A. 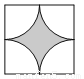 B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在△ABC中, 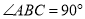 ,
, 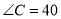 °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至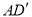 ,连接
,连接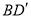 .已知AB
.已知AB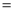 2cm,设BD为x cm,B
2cm,设BD为x cm,B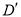 为y cm.
为y cm.
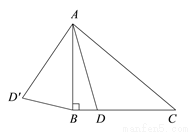
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了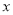 与
与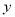 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段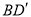 的长度的最小值约为__________
的长度的最小值约为__________ 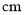 ;
;
若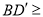
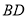 ,则
,则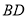 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com