
在实数0、π、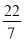 、
、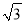 、﹣
、﹣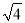 、3.1010010001中,无理数的个数有( )
、3.1010010001中,无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】无理数是无限不循环小数,根据无理数的定义可得在实数0、π、、、﹣、3.1010010001中,π、是无理数,故选B. 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源:2018年春人教版七年级数学下册期中测试 题型:解答题
如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2).
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场、市场、超市的坐标.

查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上期末模拟数试卷 题型:单选题
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
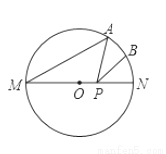
A. 2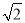 B.
B. 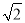 C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型:填空题
等腰三角形腰上的高与底边夹角为15°,则顶角的度数为 。
30° 【解析】根据直角三角形的两个锐角互余,得它的底角是90°-15°, 再根据等腰三角形的两个底角相等以及三角形的内角和是180°,得它的顶角是180°-2(90°-15°)=30°查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型:单选题
如果点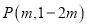 在第四象限,那么
在第四象限,那么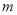 的取值范围是( ).
的取值范围是( ).
A. 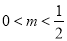 B.
B. 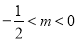 C.
C. 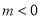 D.
D. 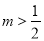
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
已知ax=-2,ay=3.求:
(1)ax+y的值;
(2)a3x的值;
(3)a3x+2y的值.
(1)-6;(2)-8;(3)-72 【解析】试题分析:(1)逆运用同底数幂相乘,底数不变指数相加解答; (3)逆运用幂的乘方,底数不变指数相乘解答; (3)逆运用幂的乘方和同底数幂的乘法进行计算即可得解. 试题解析:(1)ax+y=ax•ay=-2×3=-6; (2)a3x=(ax)3=(-2)3=-8; (3) a3x+2y=(a3x)•(a2y) =...查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于________.
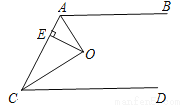
查看答案和解析>>
科目:初中数学 来源:山东省滨州市部2017-2018学年八年级(上)第一次月考数学试卷 题型:解答题
如图:点E是∠AOB的平分线上一点,ED⊥OA,EC⊥OB,垂足分别为C、D.
求证:(1)OC=OD;
(2)OE是线段CD的垂直平分线.
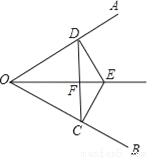
查看答案和解析>>
科目:初中数学 来源:广西崇左市天等县2017年中考数学一模试卷 题型:单选题
下列计算正确的是( )
A. ab•ab=2ab B. (2a)3=2a3
C. 3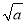 ﹣
﹣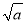 =3(a≥0) D.
=3(a≥0) D. 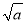 ?
?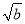 =
=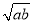 (a≥0,b≥0)
(a≥0,b≥0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com