练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，小明在大楼30米高（即PH=30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．

    （1）山坡坡角（即∠ABC）的度数等于_____度；

    （2）求山坡A、B两点间的距离（结果精确到0.1米）．

    （参考数据：≈1.414，≈1.732）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级下学期期中考试数学试卷 题型：解答题

    如图所示，点B、E、C、F在一条直线上，AB = DF，AC = DE，BE = CF．

    求证: （1） △ABC ≌ △DFE ；

    （2）连接AF、BD，求证：四边形ABDF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：山东省烟台龙口市2017-2018学年七年级下学期期中考试数学试卷 题型：单选题

    下列各方程哪个是二元一次方程（ ）

    A. 8x－y＝y B. xy＝3 C. 2x2－y＝9 D.

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市白云区钟落潭镇、江高、永平联片2017-2018学年七年级第二学期期中学情调查数学试卷 题型：单选题

    下列说法正确的是（　　）

    A. 3是9的立方根 B. 3是（﹣3）2的算术平方根

    C. （﹣2）2的平方根是2 D. 8的平方根是±4

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级中考数学一模试卷 题型：解答题

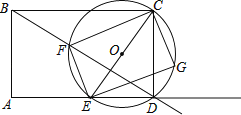
    如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

    （1）试说明四边形EFCG是矩形；

    （2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，

    ①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；

    ②求点G移动路线的长．

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级中考数学一模试卷 题型：填空题

    已知圆锥的底面半径为5cm，侧面积为65πcm2，圆锥的母线是_____cm．

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级中考数学一模试卷 题型：单选题

    若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（　　）

    A. k＞﹣1 B. k＞﹣1且k≠0 C. k＜1 D. k＜1且k≠0

    查看答案和解析>>

    科目：初中数学 来源：江西省新余市2017-2018学年八年级下学期期中考试数学试卷 题型：解答题

    先化简，再求值： ，其中 .

    查看答案和解析>>

    科目：初中数学 来源：山东蒙阴县2017-2018学年度下学期七年级期中考试数学试卷 题型：解答题

    （1）问题发现

    如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．

    请把下面的证明过程补充完整：

    证明：过点E作EF∥AB，

    ∵AB∥DC（已知），EF∥AB（辅助线的作法），

    ∴EF∥DC

    ∴∠C= ．

    ∵EF∥AB，∴∠B= ，

    ∴∠B+∠C= .

    即∠B+∠C=∠BEC．

    （2）拓展探究

    如果点E运动到图②所示的位置，其他条件不变，求证：∠B+∠C=360°﹣∠BEC．

    （3）解决问题

    如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A=　 　．（直接写出结论，不用写计算过程）

    查看答案和解析>>

    同步练习册答案