
已知a、b分别是一元二次方程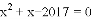 的不相等的两根,求a2+2a+b的值。
的不相等的两根,求a2+2a+b的值。
科目:初中数学 来源:江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型:填空题
若|x-2|+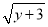 =0,则
=0,则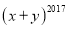 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
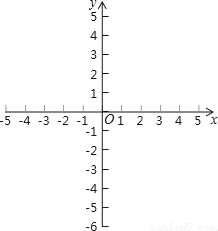
【答案】(1)画图见解析;(2)A(﹣2,0)B(0,4);(3)4;(4)x<﹣2.
【解析】试题分析:(1)求得一次函数y=2x+4与x轴、y轴的交点坐标,利用两点确定一条直线就可以画出函数图象;(2)由(1)即可得结论;(3)通过交点坐标根据三角形的面积公式即可求出面积;(4)观察函数图象与x轴的交点就可以得出结论.
试题解析:(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示
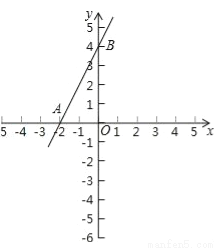
(2)由上题可知A(﹣2,0)B(0,4),
(3)S△AOB=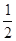 ×2×4=4,
×2×4=4,
(4)x<﹣2.
考点:一次函数图象与系数的关系;一次函数的图象.
【题型】解答题
【结束】
21
在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
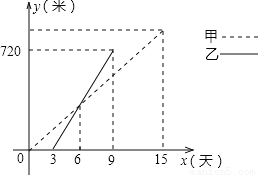
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
(1)乙工程队每天修公路120米;(2)y甲=60x,y乙=120x-360;(3)该项工程由甲、乙两工程队一直合作施工,需9天完成. 【解析】试题分析:(1)根据图象得出乙每天修的米数;(2)根据待定系数法求出函数解析式;(3)首先求出总的路程,然后计算. 试题解析:(1)∵720÷(9-3)=120∴乙工程队每天修公路120米. (2)设y乙=kx+b,则∴∴y乙=120x-...查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:单选题
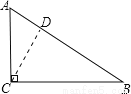
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A) (B)
(B) (C)9 (D)6
(C)9 (D)6
【答案】A
【解析】
试题分析:根据题意画出相应的图形,如图所示,在Rt△ABC中,由AC及BC的长,利用勾股定理求出AB的长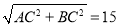 ,然后过C作CD⊥AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,即
,然后过C作CD⊥AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,即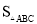 =
=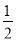 AC•BC=
AC•BC=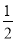 AB•CD,将AC,AB及BC的长代入求出CD的长
AB•CD,将AC,AB及BC的长代入求出CD的长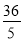 ,即为C到AB的距离.
,即为C到AB的距离.
故选A
考点:勾股定理,三角形的面积
【题型】单选题
【结束】
4
已知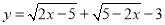 ,则2xy的值为
,则2xy的值为
A. -15 B. 15 C. -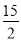 D.
D. 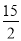
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知关于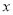 的一元二次方程
的一元二次方程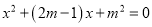 有两个实数根
有两个实数根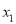 和
和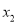 .
.
(1)求实数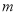 的取值范围;
的取值范围;
(2)当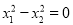 时,求
时,求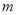 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:填空题
设α,β是一元二次方程x2+3x﹣7=0的两个根,则α2+4α+β=________.
4 【解析】试题分析:由一元二次方程根与系数的关系x1+x2=-,x1•x2=,以及一元二次方程的解,由α,β是一元二次方程x2+3x﹣7=0的两个根,可求出α+β=﹣3,α2+3α﹣7=0,即α2+3α=7,然后代入可求解为:α2+4α+β=α2+3α+α+β=7﹣3=4, 故答案为:4.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
已知α、β是方程2x2﹣3x﹣1=0的两个实数根,则(α﹣2)(β﹣2)的值是( )
A.  B.
B. 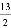 C. 3 D.
C. 3 D. 
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:2x2+5x﹣3=0.(因式分解法)
x1=,x2=﹣3. 【解析】x2+5x﹣3=0, (2x﹣1)(x+3)=0, 2x﹣1=0或x+3=0, 所以x1=,x2=﹣3.查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
点P(﹣2,3)将点P绕点O逆时针旋转90°,则P的坐标为 .
(﹣3,2) 【解析】 试题分析:如图,作PQ⊥y轴于点Q,由P点坐标得PQ=2,OQ=3,把△OPQ绕点O逆时针旋转90°得到△OP′Q′,根据旋转的性质得∠QOQ′=90°,∠OQ′P′=∠OQP=90°,P′Q′=PQ=2,OQ′=OQ=3,然后根据第二象限点的坐标特征可写出P′点的坐标. 【解析】 如图,作PQ⊥y轴于点Q, ∵点P坐标为(﹣2,3), ∴P...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com