
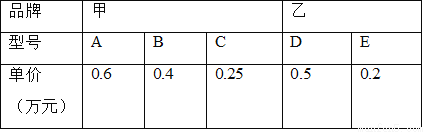
一商场有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,某中学准备从甲、乙两种品牌的电脑中各选购一种型号的电脑安装到各班教室.
(1)写出所有选购方案(利用树状图或列表法表示);
(2)若(1)中各种选购方案被选中的可能性相同,那么A型号被选中的概率是多少?
(3)已知该中学用18万元人民币购买甲、乙两种品牌电脑刚好32台(价格如下表所示,单位:万元),其中甲品牌电脑选为A型号,求该中学购买到A型号电脑多少台?
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:单选题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2.其中正确的结论是( )
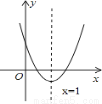
A.①② B.①③ C.①③④ D.①②③④
C 【解析】 试题分析:①图象开口向上,对称轴在y轴右侧,能得到:,,则,正确; ②∵对称轴为直线x=1,∴x=2与x=0时的函数值相等,∴当x=2时,y=4a+2b+c>0,错误; ③当x=-1时,y=a-b+c>0,正确; ④∵a-b+c>0,∴a+c>b;∵当x=1时,y=a+b+c<0,∴a+c<-b;∴b<a+c<-b, ∴|a+c|<|b|,∴,正确. 所以正...查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:解答题
化简求值 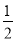 x﹣2(x﹣
x﹣2(x﹣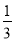 y)+(﹣
y)+(﹣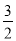 x+
x+ 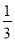 y),其中x=﹣2,y=
y),其中x=﹣2,y=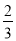 .
.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:单选题
2013年5月31日是第26个“国际无烟日”,这一天小敏与小伙伴们对人们“在娱乐场所吸烟”所持的三种态度(彻底禁烟、建立吸烟室、无所谓)进行调查,丙把调查结果绘制成了如图所示的扇形统计图,小红看了说这个图有问题,你认为( )
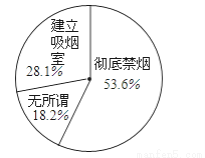
A. 没问题 B. 有问题,看不出调查了多少人
C. 有问题,赞成禁烟的还不够多 D. 有问题,所有百分数的和不等于1
D 【解析】观察扇形统计图发现这个图形有问题,所有百分数之和不等于1. 【解析】 观察扇形统计图得:28.1%+18.2%+53.6%=99.9%≠100%, 则这个图有问题,所有百分数的和不等于1. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(十) 题型:解答题
综合与探究:
如图,抛物线y=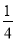 x2﹣
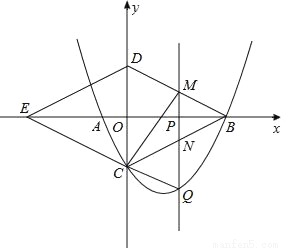
x2﹣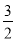 x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(十) 题型:填空题
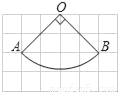
如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为_____.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(十) 题型:单选题
如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,则下列结论正确的是( )
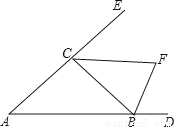
A. 点F在BC边的垂直平分线上 B. 点F在∠BAC的平分线上
C. △BCF是等腰三角形 D. △BCF是直角三角形
B 【解析】试题分析:此题主要考查角平分线的性质定理和逆定理.关键是掌握角平分线的性质:角的平分线上的点到角的两边的距离相等.如图,过点F分别作AE、BC、AD的垂线FP、FM、FN,P、M、N为垂足.根据角平分线的性质可得FP=FM,FM=FN.进而得到FP=FN,故点F在∠DAE的平分线上.过点F分别作AE、BC、AD的垂线FP、FM、FN,P、M、N为垂足,由CF是∠BCE的平分线,可...查看答案和解析>>
科目:初中数学 来源:安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型:填空题
在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有______个.
8 【解析】试题分析:在x轴的正半轴和y轴的正半轴上各有2个,在x轴的负半轴和y轴的负半轴上各有1个,总计有6个.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:解答题
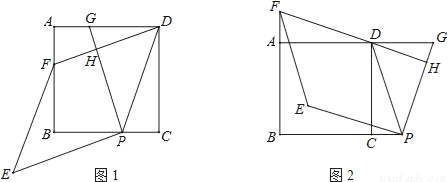
已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com