练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E.

    当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE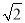＝OC；

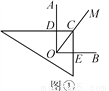
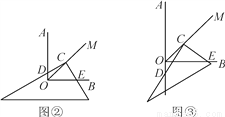
    当三角板绕点C旋转到CD与OA不垂直时，即在图②，图③这两种情况下，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段OD，OE，OC之间又有怎样的数量关系？请写出你的猜想，不需证明．

    　　

    图②中OD＋OE＝OC成立．证明见解析;图③不成立，有数量关系：OE－OD＝OC 【解析】试题分析：当三角板绕点C旋转到CD与OA不垂直时，易得△CKD≌△CHE，进而可得出证明；判断出结果．解此题的关键是根据题意找到全等三角形或等价关系，进而得出OC与OD、OE的关系；最后转化得到结论． 试题解析：图②中OD＋OE＝OC成立． 证明：过点C分别作OA，OB的垂线，垂足分别为P，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    甲、乙两车同时从A城前往B城，甲车每小时行35千米，乙车每小时行40千米，结果乙车比甲车提前半小时到达B城。问A、B两城间的路程有多少千米？

    140千米 【解析】试题分析：设A、B两城间的路程为x千米，根据甲车每小时行35千米，乙车每小时行40千米，结果乙车比甲车提前半小时到达B城，即可列方程求解. 设A、B两城间的路程为x千米，由题意得 解得 答：A、B两城间的路程为140千米.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市宁城县2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    下列四个几何体中，从上面看得到的平面图形是四边形的是( )

    A. B. C. D.

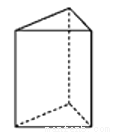    D 【解析】试题解析：A. 从上面看得到的平面图形是圆，故该选项错误； B. 从上面看得到的平面图形是三角形，故该选项错误； C. 从上面看得到的平面图形是三角形，故该选项错误； D. 从上面看得到的平面图形是四边形，正确. 故选D.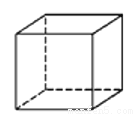

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：填空题

    已知抛物线y＝ax2＋bx＋c(a≠0)与x轴的两个交点的坐标分别是(－3，0)，(2，0)，则方程ax2＋bx＋c＝0(a≠0)的解是_________.

    .x1＝－3，x2＝2 【解析】试题解析：∵抛物线y＝ax2＋bx＋c(a≠0)与x轴的两个交点的坐标分别是(?3,0)，(2,0)， ∴当x=?3或x=2时，y=0， 即方程的解为 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：单选题

    如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；

    ②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；

    ③3a+c＞0

    ④当y＞0时，x的取值范围是﹣1≤x＜3

    ⑤当x＜0时，y随x增大而增大

    其中结论正确的个数是（　　）

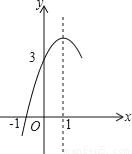
    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】解：∵抛物线与x轴有2个交点，∴b2﹣4ac＞0，所以①正确； ∵抛物线的对称轴为直线x=1，而点（﹣1，0）关于直线x=1的对称点的坐标为（3，0），∴方程ax2+bx+c=0的两个根是x1=﹣1，x2=3，所以②正确； ∵x=﹣=1，即b=﹣2a，而x=﹣1时，y=0，即a﹣b+c=0，∴a+2a+c=0，所以③错误； ∵抛物线与x轴的两点坐标为（﹣1，0）...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：解答题

    如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．

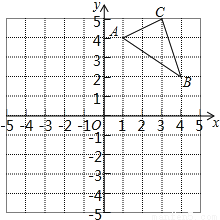
    （1）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A1B1C1；

    （2）求出点B旋转到点B1所经过的路径长．

    （1）见解析；（2）π． 【解析】 试题分析：（1）根据旋转的性质，可得答案； （2）根据线段旋转，可得圆弧，根据弧长公式，可得答案． 【解析】 （1）如图： ； （2）如图2： ， OB==2， 点B旋转到点B1所经过的路径长=π．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：填空题

    从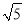－，0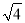， ，π，3.5这五个数中，随机抽取一个，则抽到无理数的概率是__ _．

    【解析】根据无理数的意义和特点，可知无理数有－和π，故可求得抽到无理数的概率是. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：填空题

    如图，矩形ABCD的一边BC与⊙O相切于G，DC=6，且对角线BD经过圆心O，AD交⊙O于点E，连接BE，BE恰好是⊙O的切线，已知点P在对角线BD上运动，若以B、P、G三点构成的三角形与△BED相似，则BP=______．

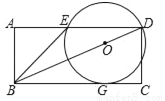
    4或12． 【解析】连接OE、OG、DG，如图，GO的延长线交AD于H， ∵BE和BG为⊙O的切线， ∴BG=BE，OB平分∠GBE，OG⊥BC， 而BC∥AD， ∴GH⊥AD， ∴EH=DH， 易得四边形CDHG为矩形， ∴CG=DH， ∴DE=2CG， ∵∠EDB=∠CBD， ∴∠EBD=∠EDB， ∴EB=ED， ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：解答题

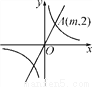
    如图，在平面直角坐标系xOy中，正比例函数y＝kx的图象与反比例函数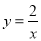的图象有一个交点为A(m，2)．

    (1)求m的值及正比例函数y＝kx的表达式；

    (2)试判断点B(2，3)是否在正比例函数图象上，并说明理由．

    (1)m＝1，正比例函数的表达式为y＝2x；(2)点B(2，3)不在正比例函数图象上，理由见解析． 【解析】试题分析：（1）将A（m，2）点代入反比例函数y= y＝，即可求得m的值； （2）将A点坐标代入正比例函数y=kx，即可求得正比例函数的解析式； （3）将x=2代入（2）中所求的正比例函数的解析式，求出对应的y值，然后与3比较，如果y=3，那么点B（2，3）是否在正比例函数...

    查看答案和解析>>

    同步练习册答案