练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

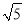    从－，0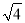， ，π，3.5这五个数中，随机抽取一个，则抽到无理数的概率是__ _．

    【解析】根据无理数的意义和特点，可知无理数有－和π，故可求得抽到无理数的概率是. 故答案为： .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    根据下列条形统计图，下面回答正确的是（ ）

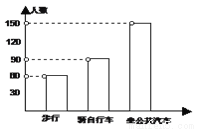
    A. 步行人数为50人 B. 步行与骑自行车的人数和比坐公共汽车的人要少

    C. 坐公共汽车的人占总数的50% D. 步行人最少只有90人

    C 【解析】A.步行人数是60人； B. 步行与骑自行车的人数和与坐公共汽车的人相等，都是150人; C. 坐公共汽车的人数占总数的150÷(60+90+150)=50%； D. 从图中可以发现：步行人数最少，但人数是60人，不是90人； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：填空题

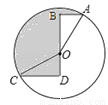
    如图，⊙O的半径为2，点A、C在⊙O上，线段BD经过圆心O，∠ABD=∠CDB=90°，AB=1，CD=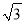，则图中阴影部分的面积为______．

    【解析】试题解析：在Rt△ABO中，∠ABO=90°，OA=2，AB=1， ∴OB= =，sin∠AOB=，∠AOB=30°． 同理，可得出：OD=1，∠COD=60°． ∴∠AOC=∠AOB+（180°-∠COD）=30°+180°-60°=150°． 在△AOB和△OCD中，有 , ∴△AOB≌△OCD（SSS）． ∴S阴影=S扇形OAC． ∴S扇形O...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：解答题

    已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E.

    当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE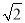＝OC；

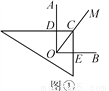
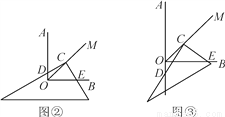
    当三角板绕点C旋转到CD与OA不垂直时，即在图②，图③这两种情况下，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段OD，OE，OC之间又有怎样的数量关系？请写出你的猜想，不需证明．

    　　

    图②中OD＋OE＝OC成立．证明见解析;图③不成立，有数量关系：OE－OD＝OC 【解析】试题分析：当三角板绕点C旋转到CD与OA不垂直时，易得△CKD≌△CHE，进而可得出证明；判断出结果．解此题的关键是根据题意找到全等三角形或等价关系，进而得出OC与OD、OE的关系；最后转化得到结论． 试题解析：图②中OD＋OE＝OC成立． 证明：过点C分别作OA，OB的垂线，垂足分别为P，...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：填空题

    如图，圆心都在x轴正半轴上的半圆O1，半圆O2，…，半圆On与直线l相切．设半圆O1，半圆O2，…，半圆On的半径分别是r1，r2，…，rn，则当直线l与x轴所成锐角为30°，且r1＝1时，r2018＝_________.

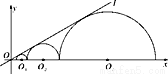
    32017 【解析】分别作O1A⊥l，O2B⊥l，O3C⊥l，如图， ∵半圆O1，半圆O2，…，半圆On与直线L相切， ∴O1A=r1，O2B=r2，O3C=r3， ∵∠AOO1=30°， ∴OO1=2O1A=2r1=2， 在Rt△OO2B中，OO2=2O2B，即2+1+r2=2r2， ∴r2=3， 在Rt△OO2C中，OO3=2O2C，即2+1+2×3++r3=2r3， ∴...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：单选题

    已知一个直角三角形的两条直角边的长恰好是方程x2－3x＝4(x－3)的两个实数根，则该直角三角形斜边上的中线长是(　　)

    A. 3 B. 4 C. 6 D. 2.5

    D 【解析】x2－3x＝4(x－3)， x2－7x+12=0 （x-3(x-4)=0, 解得，x1=3,x2=4. 由勾股定理知，斜边是5，所以斜边上中线是2.5.故选D.

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：解答题

    已知函数y=（m+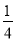）x2+（2m﹣1）x﹣3．求证：不论m为何值，该函数图象与x轴必有交点．

    证明见解析． 【解析】试题分析：一次函数图象上点的坐标特征以及抛物线与x轴的交点，分该函数为一次函数和二次函数两种情况，寻找函数图象与x轴的交点个数是解题的关键． 试题解析： 证明：当m+=0，即m=﹣时，原函数为一次函数y=﹣x﹣3， 令y=﹣x﹣3=0，解得：x=﹣2， ∴当m=﹣时，函数y=（m+）x2+（2m﹣1）x﹣3与x轴的交点坐标为（﹣2，0）； ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：解答题

    如图，在矩形ABCD中，BC＝20 cm，P，Q，M，N分别从A，B，C，D出发，沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ＝x cm(x≠0)，则AP＝2x cm，CM＝3x cm，DN＝x2 cm，

    (1)当x为何值时，点P，N重合；

    (2)当x为何值是，以P，Q，M，N为顶点的四边形是平行四边形．

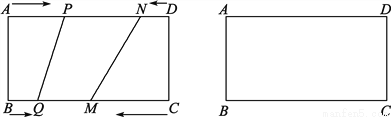
    (1) 当时，P，N重合;(2) 当x＝2或x＝4时，以P，Q，M，N为顶点的四边形是平行四边形. 【解析】试题分析：（1）当P、N重合时有：AP+DN= 20,解方程可得. (2)MQ=PN,时PQMN是平行四边形,其中不确定P，N的位置关系，所以需要分类讨论. 试题解析： (1)当P、N重合时有：AP+DN=AD=20, 即：x2+2x-20=0，解得： （舍去）...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：单选题

    已知一次函数y＝kx＋b，当0≤x≤2时，对应的函数值y的取值范围是－2≤y≤4，则kb的值为( )

    A. 12 B. －6 C. 6或12 D. －6或－12

    D 【解析】试题分析：（1）当k＞0时，y随x的增大而增大，即一次函数为增函数， ∴当x=0时，y=-2，当x=2时，y=4， 代入一次函数解析式y=kx+b得： ， 解得， ∴kb=3×（-2）=-6； （2）当k＜0时，y随x的增大而减小，即一次函数为减函数， ∴当x=0时，y=4，当x=2时，y=-2， 代入一次函数解析式y=kx+b得：...

    查看答案和解析>>

    同步练习册答案