
如图是某城市部分街道,已知AF∥BC,EC⊥BC,EF=CF,BA∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误的时间相同,那么( )
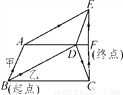
A. 甲将先到F站 B. 乙将先到F站 C. 甲、乙将同时到达 D. 不能确定
C 【解析】∵BA∥DE,BD∥AE ∴四边形ABDE是平行四边形, ∴AE=BD,AB=DE, ∵AF∥BC,EC⊥BC,EF=CF, ∴AF是EC的垂直平分线, ∴DE=CD, ∴BA+AE+EF=BD+CD+EF, ∵两车速度相同,途中耽误的时间相同, ∴甲乙两个人同时到达. 故选:C. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:辽宁省2018届九年级上学期期末模拟数学试卷 题型:单选题
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
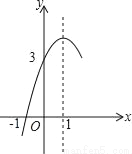
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】解:∵抛物线与x轴有2个交点,∴b2﹣4ac>0,所以①正确; ∵抛物线的对称轴为直线x=1,而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,所以②正确; ∵x=﹣=1,即b=﹣2a,而x=﹣1时,y=0,即a﹣b+c=0,∴a+2a+c=0,所以③错误; ∵抛物线与x轴的两点坐标为(﹣1,0)...查看答案和解析>>
科目:初中数学 来源:北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型:单选题
两年内某校办工厂的利润由5万元增长到9万元,设每年利润的平均增长率为x,可以列方程得 : ( )
A. 5(1+x)=9 B. 5(1+x)2=9
C. 5(1+x)+5(1+x)2=9 D. 5+5(1+x)+5(1+x)2=9
B 【解析】由题意知,5(1+x)2=9.所以选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测题 题型:填空题
如图,在矩形ABCD中,E是BC的中点,矩形ABCD的周长是20 cm,AE=5 cm,则AB的长为____cm.
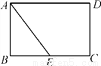
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测题 题型:单选题
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使点C与点A重合,则折痕EF的长是( )
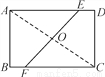
A. 7.5 B. 6 C. 10 D. 5
A 【解析】试题分析:根据矩形的性质可得AC=10,根据折叠图形可得AE=FC=AF,AO=CO=5,然后设AE=x,则BF=8-x,根据直角△ABF的勾股定理求出x的值,然后计算EF的长度.查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型:解答题
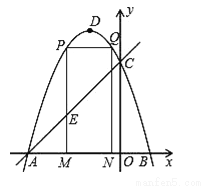
如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=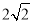 DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型:解答题
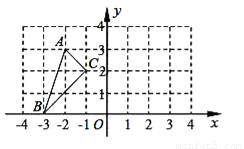
如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′;
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″;
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .
查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型:单选题
一元二次方程x2-x-2 = 0的解是( )
A. x1=1,x2=2 B. x1=1,x2=﹣2 C. x1=﹣1,x2=﹣2 D. x1=﹣1,x2=2
D 【解析】由题意x2-x-2=0, 分解因式得(x-2)(x+1)=0, 所以x-2=0,或x+1=0 即x=2或x=-1 选D.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年度上期九年级数学第三次月考试卷 题型:填空题
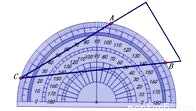
将量角器按如图所示的方式放置在三角形纸板上,使顶点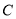 在半圆上,点
在半圆上,点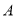 、
、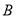 的读数分别为100°、150°,则∠ACB的大小为______度.
的读数分别为100°、150°,则∠ACB的大小为______度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com