
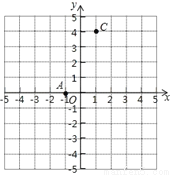
如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物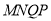 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
【答案】(1)5.6m;(2)应挪走.
【解析】试题解析:试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
试题解析:(1)如图,
在Rt△ABD中,AD=ABsin45°=4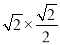 .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走.
【解析】
在Rt△ABD中,BD=ABcos45°=4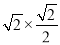 =4.
=4.
在Rt△ACD中,CD=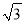 AD=4
AD=4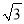 .
.
∴CB=CD-BD=4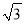 -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴货物MNQP不应挪走.
【题型】解答题
【结束】
8
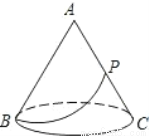
如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。 (结果不取近似数)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:解答题
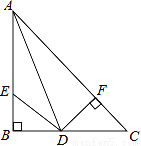
如图,△ABC中,AD为∠BAC的平分线,且DF⊥AC于F,∠B=90°,DE=DC.求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:单选题
下列等式从左到右的变形,属于因式分解的是( )
A. 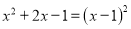 B.
B. 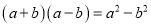
C. 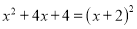 D.
D. 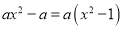
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:解答题
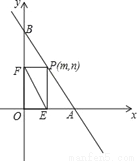
已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:填空题
设直线nx+(n+1)y=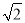 (n为自然数)与两坐标轴围成的三角形面积为Sn,则S1+S2+…+S2016的值为__.
(n为自然数)与两坐标轴围成的三角形面积为Sn,则S1+S2+…+S2016的值为__.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:单选题
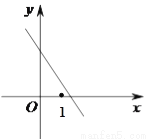
一次函数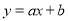 的图象如图所示,则代数式
的图象如图所示,则代数式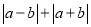 化简后的结果为( ).
化简后的结果为( ).
A. 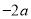 B.
B. 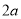 C.
C. 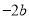 D.
D. 
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年七年级上学期第二次六校联考数学试卷 题型:填空题
已知线段AB=8cm,在直线AB上截取线段AC=2cm,则线段BC=_________cm.
6或10 【解析】① 由图示可知BC=AB-AC=8-2=6cm; ② 由图示可知BC=AB+AC=8+2=10cm, 故答案为:6或10.查看答案和解析>>
科目:初中数学 来源:内蒙古呼和浩特市土默特左旗2017-2018学年七年级(上)期中数学试卷 题型:解答题
计算题:
(1)12﹣(﹣18)+(﹣7)﹣15
(2)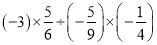
(3)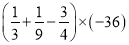
(4)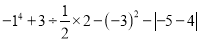 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com