
已知二次函数y = x2 +4x +3.
(1)用配方法将y = x2 +4x +3化成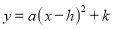 的形式;
的形式;
(2)在平面直角坐标系xOy中,画出这个二次函数的图象.

科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG.其中正确的有( )
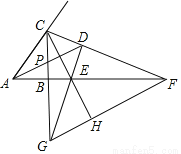
A. ①②④ B. ①②③ C. ①②④⑤ D. ①②③⑤
D 【解析】试题解析:①利用公式:∠CDA=∠ABC=45°,①正确; ②如图:延长GD与AC交于点P', 由三线合一可知CG=CP', ∵∠ADC=45°,DG⊥CF, ∴∠EDA=∠CDA=45°, ∴∠ADP=∠ADF, ∴△ADP'≌△ADF(ASA), ∴AF=AP'=AC+CP'=AC+CG,故②正确; ③如图: ∵∠EDA=...查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
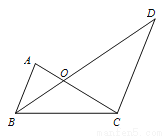
如图,BO是△ABC的角平分线,延长BO至D使得BC=CD.
(1)求证:△AOB∽△COD.
(2)若AB=2,BC=4,OA=1,求OC长.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:单选题
将抛物线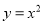 先向左平移2个单位再向下平移1个单位,得到新抛物线的表达式是( )
先向左平移2个单位再向下平移1个单位,得到新抛物线的表达式是( )
A. 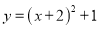 B.
B. 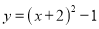
C. 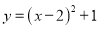 D.
D. 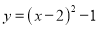
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
已知:如图,ABCD是一块边长为2米的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料. 当AM的长为何值时,截取两块相邻的正方形板料的总面积最小?

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:填空题
如图,在半径为5cm的⊙O中,如果弦AB的长为8cm,OC⊥AB,垂足为C,那么OC的长为____________cm.

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:单选题
为测量某河的宽度,小军在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E.如图所示,若测得BE=90m,EC=45m,CD=60m,则这条河的宽AB等于( )
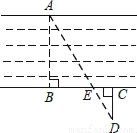
A. 120m B. 67.5m C. 40m D. 30m
A 【解析】∵∠ABE=∠DCE, ∠AEB=∠CED, ∴△ABE∽△DCE, ∴. ∵BE=90m,EC=45m,CD=60m, ∴ 故选A.查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,点P是线段AB的中点,点Q是线段AP的中点,PQ=4cm,则BQ的长度为____________ cm.
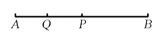
查看答案和解析>>
科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:解答题
如图所示,点A,O,B在同一条直线上,∠BOC=40°,射线OC⊥射线OD,射线OE平分∠AOC.求∠DOE的大小.
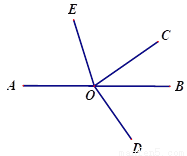
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com