练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在Rt△ABC中，∠CBA=90°，∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D，AD交CB于点P，CF交AB的延长线于点F，过点D作DE⊥CF交CB的延长线于点G，交AB的延长线于点E，连接CE并延长交FG于点H，则下列结论：①∠CDA=45°；②AF-CG=CA；③DE=DC；④FH=CD+GH；⑤CF=2CD+EG．其中正确的有（　　）

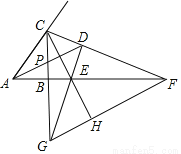
    A. ①②④ B. ①②③ C. ①②④⑤ D. ①②③⑤

    D 【解析】试题解析：①利用公式：∠CDA=∠ABC=45°，①正确； ②如图：延长GD与AC交于点P'， 由三线合一可知CG=CP'， ∵∠ADC=45°，DG⊥CF， ∴∠EDA=∠CDA=45°， ∴∠ADP=∠ADF， ∴△ADP'≌△ADF（ASA）， ∴AF=AP'=AC+CP'=AC+CG，故②正确； ③如图： ∵∠EDA=...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型：填空题

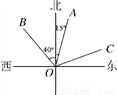
    如图，OA的方向是北偏东15°，OB的方向是北偏西40°，若∠AOC＝∠AOB，则OC的方向是__

    北偏东70° 【解析】试题分析：根据题意可知：∠AOC=∠AOB=40°+15°=55°，55°+15°=70°，则OC的方向为：北偏东70°．

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    计算:

    (1) 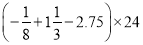(2)

    （1）-37；（2）2 . 【解析】试题分析：（1）运用乘法对加法的分配律进行计算即可求出结果； （2）先算乘方，再算乘除法，最后算加减即可得解. 试题解析：（1） = =-3+32-66 =-37； (2) =-4+3+3 =2.

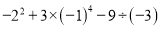
    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

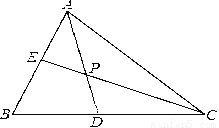
    如图，△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，AD、CE相交于点P

    (1) 求∠CPD的度数

    (2) 若AE＝3，CD＝7，求线段AC的长.

    （1）证明见解析；（2）10. 【解析】试题分析：（1）由题中条件可得△APE≌△APF，进而得出∠APE=∠APF，再利用∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，即可得出答案； （2）通过角之间的转化可得出△CPF≌△CPD，进而可得出线段之间的关系，即可得出结论． 试题解析：如图，在AC上截取AF=AE，连接PF ∵AD平分∠BAC， ∴∠BAD=...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

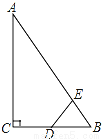
    如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为 ．

    2或3.5． 【解析】 试题分析：先求出AB的长，再分①∠BDE=90°时，DE是△ABC的中位线，然后求出AE的长度，再分点E在AB上和在BA上两种情况列出方程求解即可；②∠BED=90°时，利用∠B的余弦列式求出BE，列出方程求解即可． 【解析】 ∵∠ACB=90°，∠ABC=60°，BC=2cm， ∴AB=BC÷cos60°=2÷=4， ①∠BDE=90°时，...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    下列各多项式相乘：①（-2ab+5x）(5x+2ab);②(ax－y)(-ax-y);③(-ab-c)(ab-c);④(m+n)(-m-n).其中可以用平方差公式的有 （ ）

    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】试题解析：①（-2ab+5x）(5x+2ab)= （5x -2ab）(5x+2ab)，符合平方差公式，故①正确; ②(ax－y)(-ax-y) =- (ax－y)( ax+y)，符合平方差公式，故②正确; ③(-ab-c)(ab-c)=- (a+-c)(ab-c) ，符合平方差公式，故③正确; ④(m+n)(-m-n)=- (m+n)(m+n)，不符合平方差公式...

    查看答案和解析>>

    科目：初中数学 来源：安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型：解答题

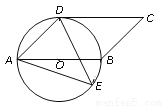
    如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED=45?．

    (1)试判断CD与⊙O的位置关系，并证明你的结论；

    (2)若⊙O的半径为3，sin∠ADE=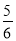，求AE的值．

    （1）CD与圆O相切，证明见解析；（2）AE=5 ． 【解析】（1）连接OD，则∠AOD=为直角，由四边形ABCD是平行四边形，则AB∥CD，从而得出∠CDO=90°，即可证出答案. （2）连接BE，则∠ADE=∠ABE，根据题意得sin∠ABE=. 由AB是圆O的直径求出AB的长.再在Rt△ABE中，求得AE即可. 【解析】 （1）CD与圆O相切． 证明：连接OD，则∠AOD...

    查看答案和解析>>

    科目：初中数学 来源：安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型：单选题

    如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为E，如果CE=2，那么AB的长是（ ）

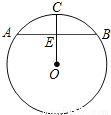
    A．4 B．8 C．6 D．10

    B 【解析】 试题分析：连接OA，由于半径OC⊥AB，利用垂径定理可知AB=2AE，又CE=2，OC=5，易求OE，在Rt△AOE中利用勾股定理易求AE，进而可求AB． 【解析】 连接OA， ∵半径OC⊥AB， ∴AE=BE=AB， ∵OC=5，CE=2， ∴OE=3， 在Rt△AOE中，AE===4， ∴AB=2AE=8， 故选B． ...

    查看答案和解析>>

    科目：初中数学 来源：北京大兴区2017-2018学年度第一学期期末检测试卷 题型：解答题

    已知二次函数y = x2 ＋4x +3.

    （1）用配方法将y = x2 ＋4x +3化成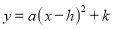的形式；

    （2）在平面直角坐标系xOy中，画出这个二次函数的图象.

    (1)y;(2)图象见解析 【解析】试题分析：(1)根据完全平方式的特点a2±2ab+b2,把一般式转化为顶点式. (2)画图象的步骤:列表、描点、连线; 【解析】 （1） （2）

    查看答案和解析>>

    同步练习册答案