
如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )
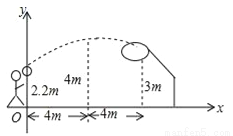
A. 比开始高0.8m B. 比开始高0.4m
C. 比开始低0.8m D. 比开始低0.4m
A 【解析】利用二次函数图象对称性知,篮圈和篮球出手的高度一样,所以人需要比开始高0.8m.故选A. 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
济南某中学足球队的18名队员的年龄如表所示:
年龄(单位:岁) |
| 12 |
| 13 |
| 14 |
| 15 |
人数 |
| 3 |
| 5 |
| 6 |
| 4 |
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
B 【解析】试题分析:∵济南某中学足球队的18名队员中,14岁的最多,有6人, ∴这18名队员年龄的众数是14岁; ∵18÷2=9,第9名和第10名的成绩是中间两个数, ∵这组数据的中间两个数分别是14岁、14岁, ∴这18名队员年龄的中位数是:(14+14)÷2=28÷2=14(岁) 综上,可得这18名队员年龄的众数是14岁,中位数是14岁. 故选:B....查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
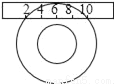
如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是_____cm.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
(1);(2)30;(3)35<x≤50. 【解析】试题分析:(1)利用单价利润件数=利润列函数关系式,按照不同条件要列分段函数,注意求定义域.(2)令函数值为12000,解方程.(3)求二次函数的增减性, y随x的增大而减小. 试题解析: 【解析】 (1)当一次购买这种产品x(x≥10)件时,销售单价为3000﹣10(x﹣10),由题意可知,3000﹣10(x﹣10)≥260...查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
如图,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15m,一面利用旧墙,其余三面用篱笆围,篱笆长为24m,若围成的花圃面积为40m2时,平行于墙的BC边长为_____m.

查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
下面四个手机应用软件图标中是轴对称图形的是 ( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
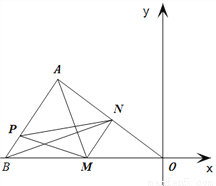
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点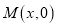 .
.
(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若 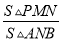 =
=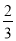 时,求此时点N的坐标.
时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:单选题
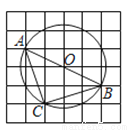
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则弧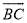 的长为( )
的长为( )
A. 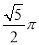 B.
B. 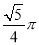 C.
C. 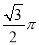 D.
D. 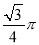
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:昌、爱、我、宜、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.我爱美 B.宜晶游 C.爱我宜昌 D.美我宜昌
C. 【解析】 试题分析:(x2﹣y2)a2﹣(x2﹣y2)b2=(x2﹣y2)(a2﹣b2)=(x﹣y)(x+y)(a﹣b)(a+b),因为x﹣y,x+y,a+b,a﹣b四个代数式分别对应爱、我,宜,昌,所以结果呈现的密码信息可能是“爱我宜昌”,故答案选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com