
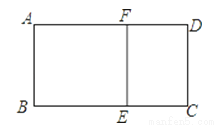
如图,矩形ABCD∽矩形ECDF,且AB=BE,求BC与AB的比值.
科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:解答题
A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。.
(1)甲、乙同时出发,背向而行,问几小时后他们相距351千米?
(2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇?
(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
(1) 5;(2);(3) 1.8小时;(4) 24小时后相遇地点距离A有72千米. 【解析】试题分析:根据相遇问题的等量关系为:两者的路程之和=相距总路程,设未知数,列方程求解即可. 试题解析:【解析】 (1)设经过x小时后他们相距351千米,根据题意得: 15x+12x=351-216 解得:x=5 答:经过5小时后他们相距351千米. (2)设相向而行,...查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第26章 反比例函数 单元检测卷 题型:单选题
三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )
A. 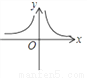 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,△ABC的三边AB、BC、CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )

A. 1:2:3 B. 2:3:4 C. 3:4:5 D. 4:5:6
D 【解析】如图,过点O作OD⊥AC于点D,作OE⊥AB于点E,作OF⊥BC于点F, ∵AO、BO、CO分别平分△ABC的三个内角, ∴OD=OE=OF, 又∵S△ABO=AB·OE,S△BCO=BC·OF,S△ACO=AC·OD, ∴S△ABO:S△BCO:S△CAO=AB·OE: BC·OF: AC·OD=AB:BC:AC, 又∵AB=40,BC=50,AC...查看答案和解析>>
科目:初中数学 来源:河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,数轴上表示1、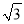 的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为 ( )
的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为 ( )
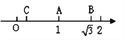
A. 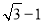 B.
B. 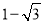 C.
C. 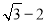 D.
D. 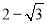
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:填空题
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
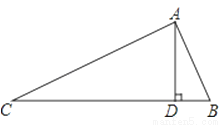
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:单选题
下列两个图形一定相似的是( )
A. 任意两个等边三角形 B. 任意两个直角三角形 C. 任意两个等腰三角形 D. 两个等腰梯形
A 【解析】试题解析:A、任意两个等边三角形一定相似,故本选项正确, B、任意两个直角三角形不一定相似,故本选项错误, C、任意两个等腰三角形不一定相似,故本选项错误, D、两个等腰梯形不一定相似,故本选项错误, 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学第一、二章综合测试卷 题型:填空题
如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM= .
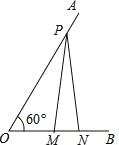
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学第五章分式与分式方程单元检测卷 题型:单选题
某人以a千米/小时的速度去相距S千米的外地送信,接着以b千米/小时的速度返回,这个人的平均速度是( )
A. 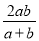 B.
B. 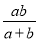 C.
C. 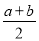 D.
D. 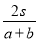
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com