练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列二次函数中，图象以直线x=2为对称轴、且经过点（0，1）的是（　　）

    A. y=（x﹣2）2+1 B. y=（x+2）2+1 C. y=（x﹣2）2﹣3 D. y=（x+2）2﹣3

    C 【解析】试题分析：采用逐一排除的方法．先根据对称轴为直线x=2排除B、D，再将点（0，1）代入A、C两个抛物线解析式： 将点（0，1）代入A中，得（x﹣2）2+1=（0﹣2）2+1=5，故A选项错误， 代入C中，得（x﹣2）2﹣3=（0﹣2）2﹣3=1，故C选项正确． 故选：C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（2）测试 题型：填空题

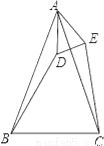
    如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD绕A旋转42°后得到的图形是______，它们之间的关系是______，其中BD=______．

    △ACE 全等 CE 【解析】△ABD绕A逆时针旋转42°后得到的图形是△ACE,它们是全等三角形,其中BD=CE,故答案为: △ACE, 全等, CE.

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：填空题

    根据天气预报，明天降水概率为20％，后天降水概率为80％，假如你准备明天或后天去放风筝，你选择___天为佳.

    明 【解析】【解析】 明天降水概率为20%＜后天降水概率为80%，放风筝应选择降水概率小的日子．故选择明天为佳．故答案为：明．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（2）测试 题型：填空题

    抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    从上表可知，下列说法中正确的是______．（填写序号）

    ①抛物线与x轴的一个交点为（3，0）； ②函数y=ax2+bx+c的最大值为6；

    ③抛物线的对称轴是直线x=；　 　　④在对称轴左侧，y随x增大而增大．

    ①③④ 【解析】试题分析：根据表格可得抛物线与x轴的交点坐标为(－2,0)和(3,0)，则①正确；根据表格可得二次函数的对称轴为直线x=，则②错误，③正确；图象开口向下，则在对称轴左侧，y随x的增大而增大，则④正确.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（2）测试 题型：填空题

    若抛物线y=ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为__________________.

    y = 【解析】试题分析：设抛物线的解析式为y=a（x-2）2+1，将点B（1，0）代入解析式即可求出a的值，从而得到二次函数解析式． 试题解析：设抛物线的解析式为y=a（x-2）2+1， 将B（1，0）代入y=a（x-2）2+1得， a=-1， 函数解析式为y=-（x-2）2+1， 展开得y=-x2+4x-3．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

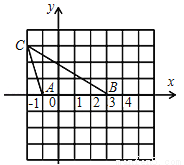
    在直角坐标系中，如图有△ABC，现另有一点D满足以A、B、D为顶点的三角形与△ABC全等，则D点坐标为 ．

    （-2，-3）、（4，3）、（4，-3）． 【解析】 试题分析：点D的可能位置如下图所示： ， 则可得点D的坐标为：（-2，-3）、（4，3）、（4，-3）．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

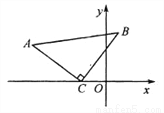
    如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为(－2，0)，若点A的坐标为(－6，3)，则点B的坐标是__________．

    (1，4) 【解析】过A和B分别作AD⊥OC于D，BE⊥OC于E， ∵∠ACB=90°， ∴∠ACD+∠CAD=90°，∠ACD+∠BCE=90°， ∴∠CAD=∠BCE， 在△ADC和△CEB中， ， ∴△ADC≌△CEB(AAS)， ∴DC=BE，AD=CE， ∵点C的坐标为(?2，0)，点A的坐标为(?6，3)， ∴OC=2，AD=C...

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

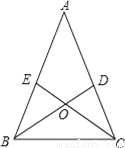
    如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E，某同学分析图形后得出以下结论，上述结论一定正确的是______（填代号）．

    ①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE．

    ①③④ 【解析】∴∠EBC=∠DCB， 又∵BD平分∠ABC，∠CE平分∠ACB， ∴∠DBC=∠ECB， ∵∠BEC=180??∠EBC?∠ECB，∠CDB=180??∠DCB?∠DBC， ∴∠BEC=∠CDB. 在△EBC和△DCB中， ， ∴△EBC≌△DCB(AAS). 即①成立； 在△BAD和△BCD中，仅有， 不满足全等的条件...

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：解答题

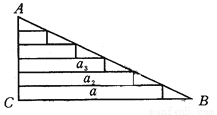
    某班在布置新年联欢会场，需要将直角三角形彩纸裁成长度不等的矩形彩条，如图所示，在Rt△ABC中，∠C=90°，AC=30cm，AB=50cm，依次裁下宽为1cm 的矩形纸条a1，a2，a3，…，若使裁得的矩形纸条的长都不小于5cm，问，每张直角三角形彩纸能裁成的矩形纸条总数是多少？

    26 【解析】试题分析：把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求解即可． 试题解析：Rt△ABC中，∠C=90°，AC=30cm，AB=50cm，由勾股定理可得BC=40cm， 设所求的矩形有x张，其中最小的矩形的长为ycm， 则 ， ∴y=40- ， 又∵y≥5， ∴40- ≥5， ∴x≤26， ∴最多能裁...

    查看答案和解析>>

    同步练习册答案