
�뽫�����¼������ĸ��ʱ���ͼ��.
(1)�׳�����������䣻
(2)��װ��3������7������Ŀڴ���ȡһ����ǡ���Ǻ���(��Щ�����ɫ����ȫ��ͬ)��
(3)��һö�ʵؾ��ȵ�Ӳ�ң�Ӳ�����º����泯��.

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������н�����2016-2017ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
����ʽ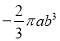 ��ϵ����_________��������_________��
��ϵ����_________��������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�IJ����п���ѧģ���Ծ� ���ͣ������
��ͼ��������y=��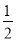 ��x+m����x��4����m��0����x���ڵ�A��B��A��B�ң�����y���ڵ�C������B��ֱ��y=
��x+m����x��4����m��0����x���ڵ�A��B��A��B�ң�����y���ڵ�C������B��ֱ��y=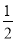 x+b��y���ڵ�D��
x+b��y���ڵ�D��
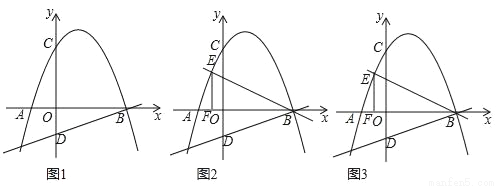
��1�����D�����ꣻ
��2����ֱ��BD��x�ᷭ�ۣ��������ߵڶ�����ͼ����һ��E������E��x�ᴹ�ߣ�����Ϊ��F����AF�ij���
��3���ڣ�2���������£���PΪ��������һ�㣬���ı���BDEPΪƽ���ı��Σ���m��ֵ����P�����꣮
��1��D��0����2������2��AF=1����3��m=3��P��2��5��. �������������������1���ɵ��ֱ���ϣ����������Ϻ�������ʽ�����뼴�ɣ� ��2�������OB��OD������������Ǻ������BF=2EF��������������4-t=2��[-��t+m����t-4��]����⼴�ɣ� ��3�����жϳ���PEQ�ա�DBO����ʾ����P��t+4��-��t+m����t-4����+2��������������������y=-��t+m����t-...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�IJ����п���ѧģ���Ծ� ���ͣ���ѡ��
��ʽ����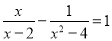 �Ľ��ǣ�������
�Ľ��ǣ�������
A. ��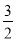 B. ��2 C. ��
B. ��2 C. ��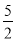 D.
D. 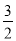
�鿴�𰸺ͽ���>>
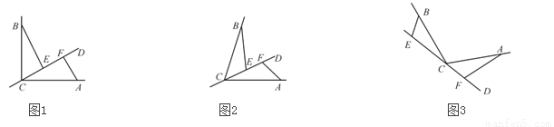
��Ŀ��������ѧ ��Դ��2018�괺��ʦ������꼶��ѧ�²��ҳ���Ծ�����ĩ���� ���ͣ������
��ͼ��CD�Ǿ�����BCA����C��һ��ֱ�ߣ�CA��CB.E��F�ֱ���ֱ��CD�����㣬�ҡ�BEC����CFA���Ϧ�.
(1)��ֱ��CD������BCA���ڲ�����E��F������CD��.
����ͼ1������BCA��90�㣬�Ϧ���90�㣬��BE CF��
����ͼ2����0�㣼��BCA<180�㣬������һ�����ڡϦ����BCA��ϵ������ ��ʹ���еĽ�����Ȼ��������˵�����ɣ�
(2)��ͼ3����ֱ��CD������BCA���ⲿ���Ϧ�����BCA�����������EF��BE��AF�����߶�������ϵ�ĺ������룺 .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺��ʦ������꼶��ѧ�²��ҳ���Ծ�����ĩ���� ���ͣ������
һ������h(m)������ʱ��n(��)֮������һ���Ĺ�ϵ����������±��е���д�� h(m)��n(��)֮��Ĺ�ϵʽ��h��____.
n(��) | 2 | 4 | 6 | 8 | 10 | �� |
h(m) | 2.6 | 3.2 | 3.8 | 4.4 | 5.0 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺��ʦ������꼶��ѧ�²��ҳ���Ծ�����ĩ���� ���ͣ���ѡ��
���û�����ͼ����������Ψһ�����ε���( )
A. ��֪�����н� B. ��֪����һ�߶Խ�
C. ��֪���Ǽ��б� D. ��֪����
B ��������A���߽DZߣ�SAS����B������һ�ǣ�SAS����C�����Ǽ�һ�ߣ�ASA����D���߱߱ߣ�SSS�����dz����ģ�ֻ��B��SSA���Ǵ���ģ� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
�۲����й������飺��3��4��5����5��12��13����7��24��25����9��40��41��������a��144��145�����е�һ�鹴������������㷢�ֵĹ��ɣ�a=_____������ʾ��5=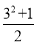 ��13=
��13=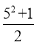 ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
��֤��������һ���ߵ������˵㵽�������ϵ��������ڵ�ֱ�ߵľ�����ȣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com