
�ס���������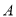 �dz���������ʻ��
�dz���������ʻ��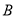 �ǣ���������ʻ�����У��ס��������뿪
�ǣ���������ʻ�����У��ס��������뿪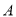 �ǵľ���
�ǵľ���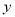 ��ǧ�ף���׳���ʻ��ʱ��
��ǧ�ף���׳���ʻ��ʱ��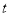 ��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ���
��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��� 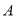 ��
�� 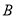 �������
�������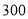 ǧ�ף����ҳ�������
ǧ�ף����ҳ�������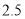 Сʱ�ϼ׳����۵��ס����������
Сʱ�ϼ׳����۵��ס����������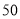 ǧ��ʱ��
ǧ��ʱ�� 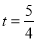 ��
��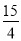 ����
����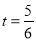 ��
��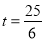 ����λΪСʱ��������ȷ�Ľ����У�������
����λΪСʱ��������ȷ�Ľ����У�������
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
C ����������ͼ����Ȼ��֪�� �� ��࣬ �����ȷ�� �� �� �����ϼ�ʱ��Ϊ�� �࣬���ҳ�������Сʱ�ϼ׳�����ڴ��� ���ס����������ʱ���ױ��ҿ죬��ʱ�һ�û������ �ױ��ҿ������Ѿ��������� �ұȼ죬���һ�û�����յ㣬�� �ұȼ������Ѿ������յ㣬�����ȷ�� ��ѡ��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���½���³ľ����2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
����������Ϊ�������ǣ� ��
A. -22 B. ��-2��2 C. -23 D. ��-2��3
B ��������A. -22 =-4�����������⣻ B. ��-2��2 =4���������⣻C. -23 =-8�����������⣻ D. ��-2��3=-8�����������⣬ ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
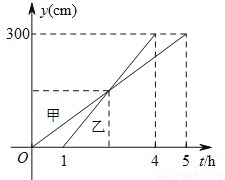
��ͼ����һ��ֽ���۵�������1=65�㣬���2�Ķ���Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݸ���2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
�Ķ����в��ϣ�
�����֪ ����
���� ��
��  ����ȷ��
����ȷ�� ��ȡֵ��Χ�������½ⷨ��
��ȡֵ��Χ�������½ⷨ��
�⣺��Ϊ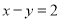 ������
������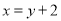 ������Ϊ
������Ϊ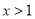 ������
������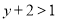 ������
������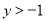 ������
������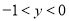 �٣�ͬ����
�٣�ͬ����  �ڣ���
�ڣ���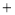 �ڵã�
�ڵã� 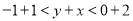 ������
������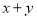 ��ȡֵ��Χ��
��ȡֵ��Χ��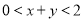 ��
��
����������ⷨ������������⣺
��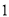 ����֪
����֪ ����
����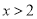 ��
�� 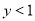 ����
���� ��ȡֵ��Χ�Ƕ��٣�
��ȡֵ��Χ�Ƕ��٣�
�� ����֪
����֪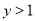 ��
�� 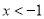 ����
����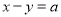 ����
����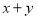 ��ȡֵ��Χ������ú�
��ȡֵ��Χ������ú�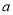 ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݸ���2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ��ʾ�� 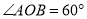 ��
�� 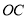 ƽ��
ƽ��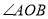 ���������
���������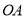 �ϵĵ�
�ϵĵ�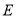 ����
����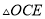 �ǵ��������Σ���ô
�ǵ��������Σ���ô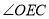 �Ķ���Ϊ__________��
�Ķ���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݸ���2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
��֪��A��a��b���ڵ������ޣ����B����a+1��3b��1���ڣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
D �����������ڵ������ޣ� �࣬ �� �֡ߣ� �� ���ڵ������ޣ� ��ѡ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
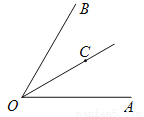
��ͼ����ABC�У�AC=BC����C=90�㣬��D��AB���е�.
��1����ͼ1������E��F�ֱ���AC��BC�ϵĵ㣬��AE=CF�����б��DEF����״����˵�����ɣ�
��2������E��F�ֱ���CA��BC�ӳ����ϵĵ㣬��AE=CF����1���еĽ����Ƿ���Ȼ��������
˵������.
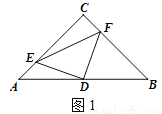
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
һ�κ���y=kx+b(k��0)��ͼ����ͼ��ʾ����һԪһ�β���ʽ-kx+b>0�ĵĽ⼯Ϊ�� ��
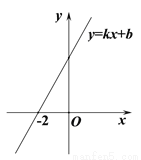
A. 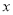 ��-2 B.
��-2 B. 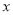 ��-2 C.
��-2 C. 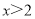 D.
D. 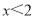
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�˱���2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
�� ��ô
��ô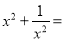 __________.
__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com