
如图,把图①中的△ABC经过一定的变换得到图②中的△A′B′C′,如果图①中△ABC上点P的坐标为(a,b),那么这个点在图②中的对应点P′的坐标为( )
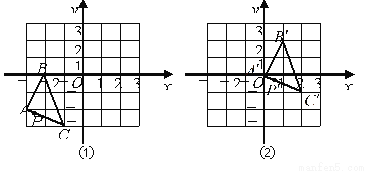
A. (a-2,b-3) B. (a-3,b-2) C. (a+3,b+2) D. (a+2,b+3)
C 【解析】观察图形可知,△ABC经过向右平移3个单位长度,再向上平移2个单位长度得到△A'B'C',所以点P'的坐标为(a+3,b+2).故选C.科目:初中数学 来源:山东省临沂市沂水县2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为
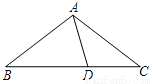
A. 40° B. 36° C. 30° D. 25°
B 【解析】设∠B=x,因AB=AC,根据等腰三角形的性质可得∠B=∠C=x,因AD=CD,根据等腰三角形的性质可得∠DAC=∠C=x,因BD=BA,根据等腰三角形的性质和三角形外角的性质可得∠BAD=∠ADB=2x,在△ABD中,根据三角形的内角和定理可得x+2x+2x=180°,解得x=36°,即∠B=36°,故选B.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
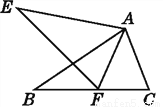
A. 1个 B. 2个 C. 3个 D. 4个
查看答案在平面直角坐标系中.点P(1,﹣2)关于x轴对称的点的坐标是( )
A. (1,2) B. (﹣1,﹣2) C. (﹣1,2) D. (﹣2,1)
查看答案如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于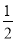 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
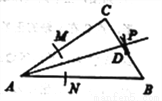
A. 15 B. 30 C. 45 D. 60
查看答案下列条件中,不能判定两个直角三角形全等的是( )
A. 两直角边对应相等 B. 斜边和一条直角边对应相等
C. 两锐角对应相等 D. 一个锐角和斜边对应相等
查看答案一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为( )
A. 7 B. 8 C. 9 D. 10
查看答案 试题属性 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
查看答案和解析>>
科目:初中数学 来源:北师大版七年级上册 第三章 整式及其加减 3.3 整式 同步测试卷 含答案 题型:填空题
(1)2x2-3x-1中,二次项是________,二次项系数是________;
一次项是________,一次项系数是________;常数项是________.
(2)3a2b2-2ab2+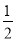 ab-1是________次多项式,它有________项,故是________次________项式.
ab-1是________次多项式,它有________项,故是________次________项式.
查看答案和解析>>
科目:初中数学 来源:人教版数学七年级下册(贵州专版) 期中综合检测 题型:解答题
如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.
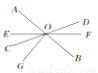
求:(1)∠DOB的度数;
(2)∠BOF的度数;
(3)∠EOG的度数.
(1)∠DOB=60°;(2)∠BOF =40°; (3)∠EOG=50°. 【解析】试题分析: (1)首先根据垂直定义可得∠GOB=90°,根据平角定义可得∠COG+∠DOB=90°,再根据∠DOB是它余角的2倍可得∠DOB+∠DOB=90°,进而可算出∠DOB的度数; (2)首先根据对顶角相等可得∠AOC的度数,再根据∠AOE=2∠DOF可得3∠COE=60°,继而可得∠COE=2...查看答案和解析>>
科目:初中数学 来源:人教版数学七年级下册(贵州专版) 期中综合检测 题型:填空题
在平面直角坐标系中,点A的坐标是(2,- 3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是____.
(-2,3) 【解析】试题分析:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,∴A′的坐标为:(2,3),∵点A′关于y轴的对称点,得到点A″,∴点A″的坐标是:(﹣2,3).故答案为:﹣2;3.查看答案和解析>>
科目:初中数学 来源:人教版数学七年级下册(贵州专版) 期中综合检测 题型:单选题
点P是直线l外一点,点A,B,C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( )
A. 6 B. 8 C. 小于6的数 D. 不大于6的数
D 【解析】在PA,PB,PC中PC最小, 若PC垂直l,则PC是垂线段, P到l的距离就是PC=6, 若PC不垂直l, 则PC大于垂线段的长度, P到l的距离小于PC=6. 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
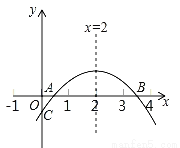
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 -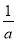 ,其中正确的结论个数有_____________________ (填序号)
,其中正确的结论个数有_____________________ (填序号)
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期4.3角同步练习 题型:填空题
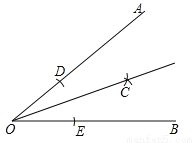
如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于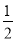 DE的长为半径画弧,在∠AOB内两弧交于点C;
DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为______.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.2中心对称图形 测试 题型:单选题
下列说法中,正确的是( ).
A. 等腰梯形既是中心对称图形又是轴对称图形.
B. 平行四边形的邻边相等.
C. 矩形是轴对称图形且有四条对称轴.
D. 菱形的面积等于两条对角线长乘积的一半.
D 【解析】等腰梯形是轴对称图形,但不是中心对称图形,所以A选项说法错误; 平行四边形的邻边不一定相等,所以B选项说法错误; 矩形是轴对称图形且有2条对称轴,所以C选项说法错误; 菱形的面积等于它两条对角线长的乘积的一半,所以D选项正确. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com