练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    由四舍五入法得到的近似数8.8×103，下列说法中正确的是 ( )

    A. 精确到十分位 B. 精确到个位 C. 精确到百位 D. 精确到千位

    C 【解析】试题解析：个位代表千，那么十分位就代表百， 精确到百位. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为（  ）

    A. 44×108 B. 4.4×109 C. 4.4×108 D. 4.4×1010

    B 【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数． 【解析】 4 400 000 000=4.4×109， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：单选题

    如果点A、B、C、D所对应的数为a、b、c、d，则a、b、c、d的大小关系是（　　）

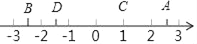
    A. a＜c＜d＜b B. b＜d＜a＜c C. b＜d＜c＜a D. d＜b＜c＜a

    C 【解析】数轴上右边的点表示的数大于左边的点所表示的数，所以b＜d＜c＜a. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：填空题

    已知A、B、C三点在同一条直线上，M、N分别为线段AB、BC的中点，且AB=60，BC=40，则MN的长为____．

    10或50 【解析】试题解析： (1)当C在线段AB延长线上时,如图1， ∵M、N分别为AB、BC的中点， ∴MN=50. (2)当C在AB上时，如图2， 同理可知BM=30，BN=20， ∴MN=10， 所以MN=50或10， 故答案为：50或10.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：单选题

    有理数m，n在数轴上的位置如图所示，则化简│n│-│m-n│的结果是（ ）

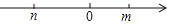
    A. m B. 2n-m C. -m D. m-2n

    C 【解析】根据数轴的特点，可知n＜0＜m，且|n|＞|m|，因此可知m-n＞0，所以根据绝对值的意义可知│n│-│m-n│=-n-m+n=-m. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

    如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．

    （1）求证：FD是⊙O的一条切线；

    （2）若AB=10，AC=8，求DF的长．

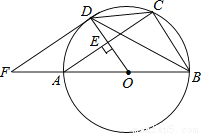
    （1）证明见解析；（2）． 【解析】试题分析：（1）利用圆周角定理以及平行线的判定得出∠FDO=90°，进而得出答案； （2）利用垂径定理得出AE的长，再利用相似三角形的判定与性质得出FD的长． （1）证明：∵∠CDB=∠CAB，∠CDB=∠BFD， ∴∠CAB=∠BFD， ∴FD∥AC（同位角相等，两直线平行）， ∵∠AEO=90°， ∴∠FDO=90°...

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：填空题

    在平面直角坐标系中，将抛物线C1：y=x2绕点（1，0）旋转180°后，得到抛物线C2，定义抛物线C1和C2上位于﹣2≤x≤2范围内的部分为图象C3．若一次函数y=kx+k﹣1（k＞0）的图象与图象C3有两个交点，则k的范围是：__．

    ﹣2+2＜k≤或≤k≤﹣4+6或k≥15 【解析】试题解析：如图,由题意图象的解析式为 图象是图中两根红线之间的上的部分图象. 由,则A(2,4),B(?2,?16),D(2,0). 因为一次函数y=kx+k?1(k>0)的图象与图象有两个交点 当直线经过点A时,满足条件,4=2k+k?1,解得 ②当直线与抛物线相切时,由 消去y得到 ∵△=0， 解得或 ...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    (10分)已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边△ADE.

    (1)如图①，点D在线段BC上移动时，直接写出∠BAD和∠CAE的大小关系；

    (2)如图②，点D在线段BC的延长线上移动时，猜想∠DCE的大小是否发生变化．若不变请求出其大小；若变化，请说明理由．

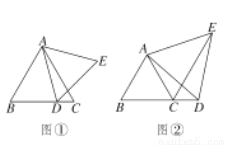
    (1)∠BAD＝∠CAE；（2）∠DCE＝60°，不发生变化． 【解析】试题分析:（1）由等边三角形的性质得出∠BAC=∠DAE，容易得出结论； （2）由△ABC和△ADE是等边三角形可以得出AB=BC=AC，AD=AE，∠ABC=∠ACB=∠BAC=∠DAE=60°，得出∠ABD=120°，再证明△ABD≌△ACE，得出∠ABD=∠ACE=120°，即可得出结论； 【解析】 ...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    如图，四边形ABCD是⊙O的内接四边形，若∠B=80°，则∠ADC的度数是（　　）

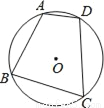
    A. 60° B. 80° C. 90° D. 100°

    D 【解析】∵四边形ABCD是⊙O的内接四边形， ∴∠ADC=180°-∠B=180°-80°=100°. 故选D.

    查看答案和解析>>

    同步练习册答案