练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若xmy6与－xym+n是同类项，则m=______,n=_______。

    1 5 【解析】由题意得 m=1，m+n=6, ∴m=1, n=5.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第二章 相交线与平行线 题型：解答题

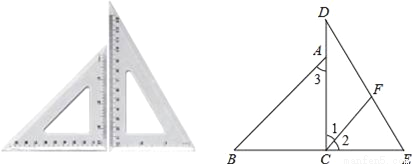
    将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

    （1）求证：CF∥AB；

    （2）求∠DFC的度数．

    （1）见解析；（2）105° 【解析】试题分析：（1）首先根据角平分线的性质可得∠1=45°，再有∠3=45°，再根据内错角相等两直线平行可判定出AB∥CF； （2）利用三角形内角和定理进行计算即可． 试题解析：（1）∵CF平分∠DCE，∴∠1=∠2=∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）； （2）...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下6.2.1 频率的稳定性 同步练习 题型：单选题

    小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:

    通话时间

    x/min

    0<x≤5

    5<x≤10

    10<x≤15

    15<x≤20

    频数

    (通话次数)

    20

    16

    9

    5

    则通话时间不超过15 min的频率为(　　)

    A. 0.1 B. 0.4 C. 0.5 D. 0.9

    D 【解析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率． 【解析】 ∵不超过15分钟的通话次数为20+16+9=45次，通话总次数为20+16+9+5=50次， ∴通话时间不超过15min的频率为=0.9， 故选D． “点睛”本题考查了频数分布表的知识，解题的关键是了解频率=频数÷样本容量，难度不大．

    查看答案和解析>>

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    右边是一个有规律排列的数表，请用含的代数式（为正整数）表示数表中第行第列的数：______________．

    【解析】第一行第n个数可用(n-1) 2+1来表示，而第一列第n个数可以用n 2来表示． 那么第n行n列的数就可用（第一行第n个数+第一列第n个数）÷2来表示， 即[(n-1)+1+n] ÷2=n 2-n+1．

    查看答案和解析>>

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    解方程：（每小题5分,共10分)

    （1）2x-3=7x-1 （2）．

    （1）x=；（2）x=-6 【解析】试题分析：（1）移项，合并同类项，系数化为1；（2）去括号，移项，合并同类项，系数化为1； 【解析】 （1）2x-3=7x-1， 2x-7x=-1+3， -5x=2， x=； （2）， 2x-6-3x+1=1, 2x-3x=1-1+6, -x=6, x=-6.

    查看答案和解析>>

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    若是关于的方程的解，则的值为( )

    A. －6 B. 2 C. 16 D. －2

    D 【解析】把代入方程得：2-a=4，解得：a=-2， 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型：解答题

    如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.

    证明见解析. 【解析】试题分析：过点C作CF∥AB，结合已知可得∠A+∠ACF=180°，再根据已知角关系可得∠D+∠FCD=180°，根据平行线的判定即可得到CF∥DE，此时再次运用平行线的判定即可解答本题. 试题解析：过点C作CF∥AB. ∵CF∥AB， ∴∠A+∠ACF=180°. ∵∠A+∠ACD+∠D=360°， ∴∠D+∠FCD=180°， ∴...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型：单选题

    如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___. 

    内错角 【解析】图中两只手的食指和拇指构成”Z“形，根据内错角是在截线两旁，被截线之内的两角，内错角的边构成”Z“形，可知答案为：内错角. 故答案为：内错角.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章三角形4.3探索三角形全等的条件 同步练习 题型：解答题

    已知在△ABC中，∠ABC=∠ACB，∠1=∠2，求证：AD平分∠BAC。

    证明见解析 【解析】试题分析：易证AB=AC和BD=CD，即可证明△ABD≌△ACD，可得∠BAD=∠CAD，即可解题． 试题解析：∵∠ABC=∠ACB， ∴AB=AC， ∵∠1=∠2， ∴BD=CD， 在△ABD和△ACD中， ， ∴△ABD≌△ACD（SSS）， ∴∠BAD=∠CAD， ∴AD平分∠BAC.

    查看答案和解析>>

    同步练习册答案