练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___. 

    内错角 【解析】图中两只手的食指和拇指构成”Z“形，根据内错角是在截线两旁，被截线之内的两角，内错角的边构成”Z“形，可知答案为：内错角. 故答案为：内错角.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册 第三章 变量之间的关系 3.1 用表格表示的变量间关系 同步练习 题型：单选题

    球的体积V(m3)与球的半径R(m)之间的关系式为V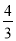＝πR3，当球的大小发生变化时，关于π、R的说法中，最准确的是( )

    A. R是常量 B. π是变量

    C. R是自变量 D. R是因变量

    C 【解析】试题解析：球的大小发生变化时， 发生变化，是变量， 是常量，不变. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    若xmy6与－xym+n是同类项，则m=______,n=_______。

    1 5 【解析】由题意得 m=1，m+n=6, ∴m=1, n=5.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型：单选题

    如图,下列推理正确的有(　　)

    ①因为∠1=∠4,所以BC∥AD;

    ②因为∠2=∠3,所以AB∥CD;　

    ③因为∠BCD+∠ADC=180°,所以AD∥BC;

    ④因为∠1+∠2+∠C=180°,所以BC∥AD.

    A. 1个 B. 2个 C. 3个 D. 4个

    A 【解析】（1）由∠1=∠2不能推导出BC∥AD，所以①中的推理错误； （2）由∠2=∠3不能推导出AB∥CD，所以②中的推理错误； （3）由∠BCD+∠ADC=180°能推导出BC∥AD，所以③中推理正确； （4）由∠BCD+∠ABC=180°不能推导出BC∥AD，所以④中推理错误； 即4个推理中，只有③正确. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型：单选题

    如图，能判定EB∥AC的条件是( )

    A. ∠C＝∠ABE B. ∠A＝∠EBD C. ∠C＝∠ABC D. ∠A＝∠ABE

    B 【解析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角，被判断平行的两直线是否由“三线八角”而产生的被截直线，因此： A、∠C=∠ABE不能判断出EB∥AC，故A选项不符合题意； B、∠A=∠EBD不能判断出EB∥AC，故B选项不符合题意； C、∠C=∠ABC只能判断出AB=AC，不能判断出EB∥AC，故C选项不符合题意； D、∠A=∠ABE，...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（2）同步练习 题型：填空题

    如图，（1）如果∠1=__________，那么DE∥AC；（同位角相等，两直线平行）；

    （2）如果∠1=__________，那么EF∥BC；（内错角相等，两直线平行）；

    （3）如果∠DEF+__________=180°，那么DE∥AC；（同旁内角互补，两直线平行）；

    （4）如果∠2+__________=180°，那么AB∥DF；（同旁内角互补，两直线平行）．

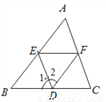
    ∠C； ∠DEF； ∠EFC； ∠AED． 【解析】（1）如果∠1=∠C ，那么DE//AC；（同位角相等，两直线平行） （2）如果∠1=∠DEF ，那么EF//BC；（内错角相等，两直线平行） （3）如果∠DEF+∠EFC =180°，那么DE//AC；（同旁内角互补，两直线平行） （4）如果∠2+∠AED =180°，，那么AB//DF；（同旁内角互补，两直线平行） ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（2）同步练习 题型：单选题

    如图，点E在BC的延长线上，下列条件中能判定BC//AD的是 ( )

    A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE

    C 【解析】A. ∵∠1=∠2 ，∴AB∥CD, 故不正确； B. ∵ ∠DAB+∠D=180° ，∴AB∥CD, 故不正确； C. ∵∠3=∠4 ，∴ BC∥AD, 故正确； D. ∵∠B=∠DCE，∴AB∥CD, 故不正确； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.5 利用三角形全等测距离 同步练习 题型：解答题

    如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.

    . 【解析】试题分析：可设计如图所示的工具,利用△AOB≌△COD即可求解. 试题解析：可设计如图所示的工具,其中O为AC,BD的中点. 在△AOB和△COD中, 所以△AOB≌△COD(SAS). 所以AB=CD.所以测量出C,D之间的距离,CD的长就是A,B间的距离. 因为AB=a-2x,所以x==.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 第四章 三角形 章节检测题 题型：解答题

    （10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD

    可证明△EBM≌△FCM， 得∠EMB≌△FCM， 得∠EMB＝∠FMC， ∵∠CMF＋∠BMF＝180° ∴∠BME＋∠BMF＝180° ∴E、F、M恰好在一直线上 【解析】分析：三角形全等条件中必须是三个元素，本题已经有两条对应边相等，只要再找到它们的夹角相等就可以了． 解答：证明：∵BE、CF分别是AC、AB两条边上的高， ∴∠ABD+∠BAC...

    查看答案和解析>>

    同步练习册答案