练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（ ）

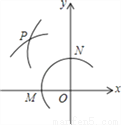
    A. a=b B. 2a+b=﹣1 C. 2a﹣b=1 D. 2a+b=1

    D 【解析】【解析】 根据作图方法可得点P在第二象限角平分线上，则P点横纵坐标的和为0，故2a+b+1=0，整理得：2a+b=﹣1，故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型：单选题

    关于x的一元二次方程x2+px-6=0的一个根为2，则p的值为（ ）

    A. -2 B. 2 C. -1 D. 1

    D 【解析】试题解析：把代入方程得 解得： 故选D.

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试九年级数学试卷 题型：解答题

    先化简,再求值： ,其中x=3.

    - 【解析】试题分析：先把代数式化简，然后再代入求值． 试题解析：原式 当x=3时,原式

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊市诸城市2016-2017学年八年级（上）期末数学试卷 题型：解答题

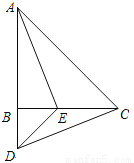
    如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC．

    ① 求证：△ABE≌△CBD；

    ② 若∠CAE＝30°，求∠BDC的度数．

    ①证明见解析②∠BDC＝75° 【解析】试题分析：（1）利用“边角边”证明△ABE≌△CBD即可；②先根据等腰直角三角形的锐角都是45°求出∠CAB，再求出∠BAE，然后根据全等三角形对应角相等求出∠BCD，再根据直角三角形两锐角互余其解即可； 试题解析： （1）证明：∵∠ABC=90°，D为AB延长线上一点， ∴∠ABE=∠CBD=90°， 在△ABE和△CBD中，...

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊市诸城市2016-2017学年八年级（上）期末数学试卷 题型：填空题

    等腰三角形一腰上的高与另一边的夹角为50°，则顶角的度数为______．

    100°或140°或40°． 【解析】【解析】 △ABC是等腰三角形，且∠BAC为顶角，CD是腰AB的高． （1）当等腰三角形是锐角三角形时，如图①； ∵∠ACD=50°，∴∠BAC=90°﹣∠ACD=40°； （2）当等腰三角形是钝角三角形时； ①如图②﹣1； 当∠BCD=50°时，∠B=40°； ∴∠BAC=180°﹣2∠B=100°； ②如图...

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊市诸城市2016-2017学年八年级（上）期末数学试卷 题型：单选题

    如图所示，有以下三个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这三个条件中任选两个作为假设，另一个作为结论，则组成真命题的个数为（　　）

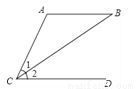
    A. 0 B. 1 C. 2 D. 3

    D 【解析】所有等可能的情况有3种，分别为①②⇒③；①③⇒②；②③⇒①，其中组成命题是真命题的情况有：①②⇒③；①③⇒②；②③⇒①， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型：解答题

    某商场用24000元购入一批空调，然后以每台3000元的价格销售，因天气炎热，空调很快售完；商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，售价每台也上调了200元．

    （1）商场第一次购入的空调每台进价是多少元？

    （2）商场既要尽快售完第二次购入的空调，又要在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售，最多可将多少台空调打折出售？

    （1）2400元；（2）8台． 【解析】试题分析：（1）设商场第一次购入的空调每台进价是x元，根据题目条件“商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，每台的售价也上调了200元”列出分式方程解答即可； （2）设最多将台空调打折出售，根据题目条件“在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售...

    查看答案和解析>>

    科目：初中数学 来源：安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型：单选题

    如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，BC＝5，EF垂直平分BC，点P为直线EF上的任一点，则AP＋BP的最小值是（　　）

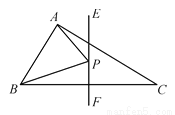
    A. 3 B. 4 C. 5 D. 6

    B 【解析】试题分析：根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可． 【解析】 ∵EF垂直平分BC， ∴B、C关于EF对称， AC交EF于D， ∴当P和D重合时，AP+BP的值最小，最小值等于AC的长， 由勾股定理得：AC==4． 故答案为：4．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

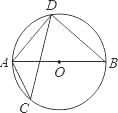
    如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为 ．

    65°． 【解析】试题分析：根据直径所对的圆周角是直角，构造直角三角形ABD，再根据同弧所对的圆周角相等，求得∠B的度数，即可求得∠BAD的度数． ∵AB为⊙O直径 ∴∠ADB=90° ∵相同的弧所对应的圆周角相等，且∠ACD=25° ∴∠B=25° ∴∠BAD=90°﹣∠B=65°．

    查看答案和解析>>

    同步练习册答案