
先化简,再求值: 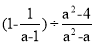 ,其中a是整数,且﹣3<a<3.
,其中a是整数,且﹣3<a<3.
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
已知点P(1,m)在第四象限,则点Q(-1,m)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】∵点P(1,m)在第四象限,∴m<0,∴点Q(-1,m)在第三象限.故选C.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
先化简,再求值:  ,其中x是不等式3x+7>1的负整数解.
,其中x是不等式3x+7>1的负整数解.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
如图,△ABC的周长为19cm,AC的垂直平分线DE交AC于点E,E为垂足,AE=3cm,则△ABD的周长为________.
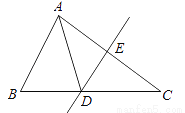
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:解答题
阅读与思考;
婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下:
已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF
证明∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同时∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中点.
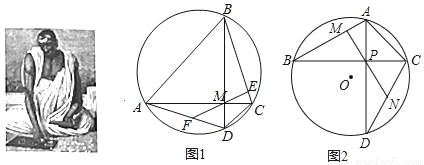
(1)请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:
已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
(2)已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
(1)证明见解析;(2)证明见解析, PN=1. 【解析】试题分析:(1)由于AC⊥BD,所以∠AMD=90°,∠FAM+∠FDM=90°,由于F是AD的中点,所以AF=MF=DF,从而可证明∠EMC+∠MCB=90°. (2)由圆周角定理得出∠D=∠B=30°,由三角形内角和定理求出∠DAC=45°,得出△APC是等腰直角三角形,∴PA=PC,∠CPD=90°,由(1)的证明过程可知...查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:填空题
计算:(﹣2)0+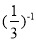 ﹣
﹣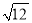 +2tan30°=_____.
+2tan30°=_____.
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
小敏的圆规摆放如图所示,则几个和小明的圆规形状一样的圆规中,与小明摆放的位似的是( )
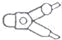
A. 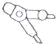 B.
B. 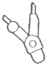 C.
C. 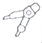 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:填空题
某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打_____折.
7 【解析】试题分析:设打x折,利用销售价减进价等于利润得到1200•﹣800≥800×5%,然后解不等式求出x的范围,从而得到x的最小值即可. 【解析】 设打x折, 根据题意得1200•﹣800≥800×5%, 解得x≥7. 所以最低可打七折. 故答案为七.查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
把抛物线y=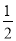 x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
A. y=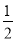 (x+1)2-3 B. y=
(x+1)2-3 B. y=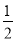 (x-1)2-3 C. y=
(x-1)2-3 C. y=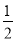 (x+1)2+1 D. y=
(x+1)2+1 D. y= (x-1)2+1
(x-1)2+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com