
阅读与思考;
婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下:
已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF
证明∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同时∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中点.
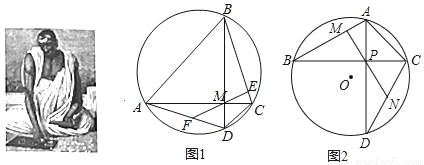
(1)请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:
已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
(2)已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
(1)证明见解析;(2)证明见解析, PN=1. 【解析】试题分析:(1)由于AC⊥BD,所以∠AMD=90°,∠FAM+∠FDM=90°,由于F是AD的中点,所以AF=MF=DF,从而可证明∠EMC+∠MCB=90°. (2)由圆周角定理得出∠D=∠B=30°,由三角形内角和定理求出∠DAC=45°,得出△APC是等腰直角三角形,∴PA=PC,∠CPD=90°,由(1)的证明过程可知... 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
若分式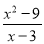 的值为0,则x的值是( )
的值为0,则x的值是( )
A. -3 B. 3 C. ±3 D. 0
A 【解析】由题意可知: ,解得:x=-3,故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的( )
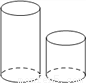
A. 主视图相同 B. 俯视图相同
C. 左视图相同 D. 主视图、俯视图、左视图都相同
B 【解析】由于主视图是从正面看的图形,俯视图是从上面看的图形,左视图是从左面看的图形,而这两个圆柱体的高不相同,所以只有它们的俯视图相同. 故选B.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
化简 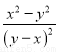 的结果是( )
的结果是( )
A. ﹣1 B. 1 C. 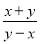 D.
D. 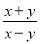
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
将直线y=2x﹣4向上平移5个单位后,所得直线的表达式是________.那么将直线y=2x﹣4沿x轴向右平移3个单位得到的直线方程是________.
y=2x+1 y=2x﹣10 【解析】【解析】 将直线y=2x﹣4向上平移5个单位后,所得直线的表达式是y=2x﹣4+5=2x+1.将直线y=2x﹣4沿x轴向右平移3个单位得到的直线方程是y=2(x-3)﹣4﹣3=2x﹣10; 故答案为:y=2x+1;y=2x﹣10.查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:解答题
先化简,再求值: 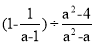 ,其中a是整数,且﹣3<a<3.
,其中a是整数,且﹣3<a<3.
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
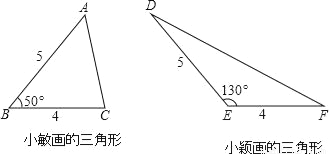
A. S△ABC>S△DEF B. S△ABC<S△DEF C. S△ABC=S△DEF D. 不能确定
C 【解析】试题解析:如图,过点A.D分别作AG⊥BC,DH⊥EF,垂足分别为G、H, 在Rt△ABG中, 在Rt△DHE中, ∴AG=DH. ∵BC=4,EF=4, 故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中,哪两个条件 可判定△ABC是等腰三角形(用序号写出所有情形);
(2)选择第(1)小题中的一种情形,证明△ABC是等腰三角形.
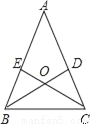
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
从图中的四张印有汽车品牌标志图案的卡片中任取一张,取出印有汽车品牌标志的图案是中心对称图形的卡片的概率是( )

A.  B.
B.  C.
C.  D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com