练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个等腰三角形的两边长分别为2 和5，则它的周长为

    A. 7 B. 9 C. 12 D. 9 或 12

    C 【解析】若腰长为2，则三边长为2，2，5，2+2<5，此时构不成三角形； 若腰长为5，则三边长为5，5，2，能构成三角形，所以周长为：5+5+2=12， 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    先化简，再求值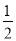． x﹣2（x﹣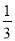y2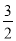）+（﹣x+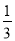y2），其中x=﹣2，y=．

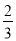    原式=﹣3x+y2，当x=﹣2，原式=6． 【解析】试题分析：根据整式的加减运算法则化简后再代入求值即可. 试题解析： 原式=x﹣2x+y2﹣x+y2 =﹣3x+y2， 当x=﹣2，y=时，原式=6．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    一球鞋厂，现打折促销卖出330双球鞋，比上个月多卖10%，设上个月卖出 双，列出方程（   ）

    A. 10%x=330           B. (1-10%)x=330             C. (1-10%)2x=330             D. (1+10%)x=330

    D 【解析】【解析】 设上个月卖出x双，根据题意得：（1+10%）x=330．故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市沂南县2016-2017上学期八年级期末数学调研试卷 题型：填空题

    如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处．若∠A=26°，则∠CDE= ．

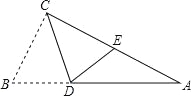
    71°． 【解析】 试题分析：∵在Rt△ABC中，∠ACB=90°，∠A=26°，∴∠B=64°， ∵将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，∠ACB=90°， ∴∠BCD=∠ECD=45°，∠CED=∠B=64°， ∴∠CDE=180°﹣∠ECD﹣∠CED=71°， 故答案为：71°．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市沂南县2016-2017上学期八年级期末数学调研试卷 题型：单选题

    如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB，垂足为E．若PE=3，则两平行线AD与BC间的距离为（　　）

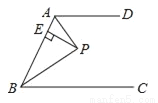
    A. 3 B. 5 C. 6 D. 不能确定

    C 【解析】试题解析：作PF⊥AD于F，PG⊥BC于G， ∵AP是∠BAD的角平分线，PF⊥AD，PE⊥AB， ∴PF=PE=3， ∵BP是∠ABC的角平分线，PE⊥AB，PG⊥BC， ∴PG=PE=3， ∵AD∥BC， ∴两平行线AD与BC间的距离为PF+PG=6， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学下册 期中测评 题型：解答题

    如图,在边长为1个单位长度的小正方形组成的网格中,已知AB∥CD,分别探讨下面三个图形中∠BAP与∠APC,∠DCP的关系,请任选一个加以说明.

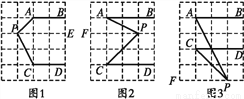
    见解析 【解析】试题分析：(1)过P作AB平行线，利用同旁内角关系证明.(2) 过P作AB平行线，利用内错角关系证明.（3）过P作AB平行线，利用内错角关系证明. 试题解析： 对图1,∠BAP+∠DCP+∠APC=360°. 证明:过P作PE∥AB, 则AB∥CD, 因为AB∥PE,所以∠PAB+∠APE=180°, 因为PE∥CD,所以∠DCP+∠CPE...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学下册 期中测评 题型：填空题

    有若干张如图所示的正方形A类、B类卡片和长方形C类卡片，如果要拼成一个长为（2a＋b），宽为（3a＋2b）的大长方形，则需要C类卡片 张．

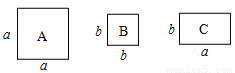
    7 【解析】试题解析：（2a+b）×（3a+2b）=6a2+7ab+2b2， 则需要C类卡片7张．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：解答题

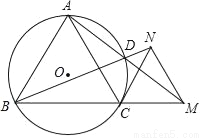
    如图，在等边△ABC中，M是边BC延长线上一点，连接AM交△ABC的外接圆于点D，延长BD至N，使得BN=AM，连接CN、MN，

    （1）求证：△CMN是等边三角形；

    （2）判断CN与⊙O的位置关系，并说明理由；

    （3）若AD：AB=3：4，BN=4，求等边△ABC的边长．

    （1）证明见解析;（2）CN是⊙O的切线,理由见解析；（3）等边△ABC的边长是3． 【解析】试题分析：（1）根据全等三角形的判定定理得到△BCN≌△ACM，由全等三角形的性质得到CN=CM，∠BCN=∠ACM，求得∠MCN=∠ACB=60°，即可得到结论； （2）根据全等三角形的性质得到∠ACO=∠BCO=ACB=30°，根据角的和差得到∠OCN=90°，根据切线的判定定理得到结论；...

    查看答案和解析>>

    科目：初中数学 来源：浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型：单选题

    如图，D是等边△ABC外接圆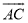上的点，且∠CAD=20°，则∠ACD的度数为（ ）

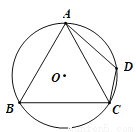
    A. 20° B. 30° C. 40° D. 45°

    C 【解析】∴∠B=60°， ∵四边形ABCD是圆内接四边形， ∴∠D=180°?∠B=120°， ∴∠ACD=180°?∠DAC?∠D=40°， 故选：C.

    查看答案和解析>>

    同步练习册答案