
下列四个图形分别是四届国际数学家大会的会标,其中属于中心对称图形的有( )

A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:根据中心对称的概念可得第一个图形是中心对称图形,第二个图形不是中心对称图形,第三个图形是中心对称图形,第四个图形不是中心对称图形,所以,中心对称图有2个.故选B. 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:黄金30题系列七年级数学 小题好拿分 题型:填空题
如图所示,已知:D是线段AB上一点,M,N分别是AD,DB的中点,则线段AB与线段MN之间的关系是___________.
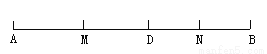
查看答案和解析>>
科目:初中数学 来源:福建省上杭县城区片2017-2018学年第一学期三校联考及答案 题型:单选题
已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )
A. 不盈不亏 B. 盈利10元 C. 亏损10元 D. 盈利50元
B 【解析】试题解析:设盈利的进价是x元, 80-x=60%x x=50 设亏本的进价是y元 y-80=20%y y=100 80+80-100-50=10元. 故赚了10元. 故选B.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-2017学年度第一学期期末教学质量检测 九年级数学试卷 题型:填空题
如图,直线y1=x+b与双曲线y2=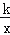 交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=
交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=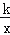 交于点C.则:
交于点C.则:
①直线AB的解析式为y1=x+3;
②B(﹣1,﹣4);
③当x>1时,y2<y1;
④当AC的解析式为y=4x时,△ABC是直角三角形.
其中正确的是 .(把所有正确结论的序号都写在横线上)
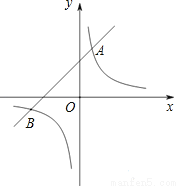
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-2017学年度第一学期期末教学质量检测 九年级数学试卷 题型:单选题
在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2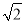 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )
A. 3π B. 4π C. 2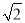 π D. 2π
π D. 2π
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:解答题
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=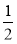 ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:填空题
如果一组数据 -2,0,3,5,x的极差是9,那么这组数据的平均数是 ____.
2.6或0.4. 【解析】 试题分析:根据极差的定义求解.分两种情况:x为最大值或最小值.再根据平均数的公式求解即可. 一组数据-2,0,5,3,x的极差是9, 当x为最大值时,x-(-2)=9,x=7,平均数是:(-2+0+5+3+7)÷5=2.6; 当x是最小值时,5-x=9,解得:x=-4,平均数是:(-2+0+5+3-4)÷5=0.4.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:解答题
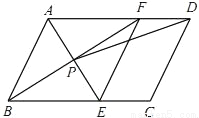
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:单选题
分式:①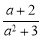 ,②
,②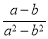 ,③
,③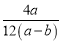 ,④
,④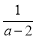 中,最简分式有( )
中,最简分式有( )
A.1个 B.2个 C.3个 D.4个
B 【解析】①④中分子分母没有公因式,是最简分式; ②中有公因式(a﹣b); ③中有公约数4; 故①和④是最简分式.故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com