
下列所述图形中,既是轴对称图形又是中心对称图形的是( )
A. 等边三角形 B. 平行四边形 C. 正五边形 D. 圆
D 【解析】试题解析:A. 是轴对称图形,不是中心对称图形,故此选项错误; B. 不是轴对称图形,是中心对称图形,故此选项错误; C. 是轴对称图形,不是中心对称图形,故此选项错误; D. 是轴对称图形,也是中心对称图形,故此选项正确; 故选D. 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源:人教版初中数学七年级下册第六章 《平方根》同步练习 题型:单选题
下列各式中,运算结果正确的是( )
A. (﹣1)3+(﹣3.14)0+2﹣1=﹣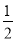 B. 2x﹣2=
B. 2x﹣2= 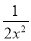
C. 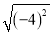 =﹣4 D. a2•a3=a5
=﹣4 D. a2•a3=a5
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《二元一次方程组》同步练习 题型:单选题
已知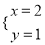 是二元一次方程组
是二元一次方程组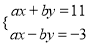 的解,则a+b的算术平方根为( )
的解,则a+b的算术平方根为( )
A. ±3 B. 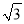 C. 3 D. 9
C. 3 D. 9
查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:单选题
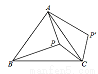
如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则cos∠PAP'的值为等于( )
A. 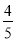 B.
B. 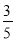 C.
C. 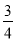 D.
D. 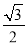
查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:单选题
如图,点A、C、B在⊙O上,已知∠AOB =∠ACB =α.则α的值为【 】

A.135° B.120° C.110° D.100°
B 【解析】分析:先运用“在同圆或等圆中,同弧或等弧所对的圆周角等于圆心角的一半”,再运用周角360°即可解. 解答:【解析】 ∵∠ACB=a ∴优弧所对的圆心角为2a ∴2a+a=360° ∴a=120°. 故选B.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
解分式方程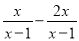 =1,可知方程的解为( )
=1,可知方程的解为( )
A. x=1 B. x=3 C. x=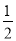 D. 无解
D. 无解
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
电动车每小时比自行车多行驶了25千米,自行车行驶30千米比电动车行驶40千米多用了1小时,求两车的平均速度各为多少?设自行车的平均速度为x千米/小时,应列方程为( )
A. 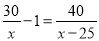 B.
B. 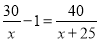
C. 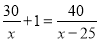 D.
D. 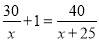
查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:单选题
将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是( )
主视图相同 B.左视图相同 C.俯视图相同 D.三种视图都不相同

查看答案和解析>>
科目:初中数学 来源:河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
(1)计算:
①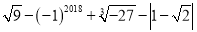
②(x-2)(x+5)-x(x+2)
(2)因式分解:
①25x3-36xy2 ②(a2+16b2)2-64a2b2
(1)①- ②x-10;(2)①x(5x+6y)(5x-6y) ②(a+4b)2(a-4b)2 【解析】试题分析: (1)①按实数的相关运算法则计算即可;②按多项式乘法法则计算即可; (2)①先提公因式,再用“平方差公式”分解即可;②先用“平方差公式”分解,再用“完全平方公式”分解即可. 试题解析: (1)①原式=; ②原式=; (2)①原式= ; ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com