
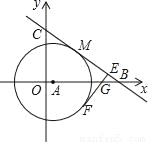
��ͼ����ƽ��ֱ������ϵ�У���֪��A��x�����ᣬ�Ե�AΪԲ������A����M��4��4���ڡ�A�ϣ�ֱ��y=��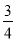 x+b��Բ�����ڵ�M���ֱ�x�ᡢy����B��C���㣮
x+b��Բ�����ڵ�M���ֱ�x�ᡢy����B��C���㣮
��1��ֱ��д��b��ֵ�͵�B�����ꣻ
��2�����A�������Բ�İ뾶��
��3����EF�С�A�ڵ�F�ֱ�AB��BC��G��E����FE��BC����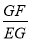 ��ֵ��
��ֵ��
 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ���һ ���ͣ������
��ͼ1��PΪ��MONƽ����OC��һ�㣬��PΪ����ġ�APB���߷ֱ�������OM��ON����A��B���㣬�����APB���Ƶ�P��תʱʼ������OA•OB=OP2 �� ���ǾͰѡ�APB������MON�Ĺ����ǣ�
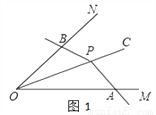
��1����ͼ2��PΪ��MONƽ����OC��һ�㣬��P��PB��ON��B��AP��OC��P����ô��APB________��MON�Ĺ����ǣ���ǡ����ǡ�����
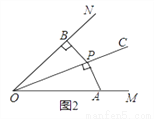
��2������ͼ3�������MON=60�㣬OP=2����APB�ǡ�MON�Ĺ����ǣ�����AB�����AOB������͡�APB�Ķ�����
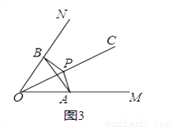
�������MON=���㣨0�㣼���㣼90�㣩��OP=m����APB�ǡ�MON�Ĺ����ǣ�ֱ���ú��Ц���m�Ĵ���ʽ��ʾ��AOB�������
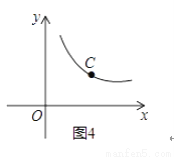
��3����ͼ4����C�Ǻ���y=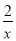 ��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ����ǡ�APB�Ķ���P�����꣮
��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ����ǡ�APB�Ķ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��29�� ͶӰ����ͼ ��Ԫ���� ���ͣ���ѡ��
��ͼ�ǽ���������ȥһ���Ǻ��γɵļ�����,��ü����������ͼΪ( )
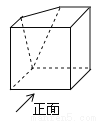
A.  B.
B.  C.
C. 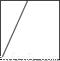 D.
D. 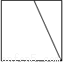
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ� ��13�� ��Գ� ��Ԫ���Ծ� ���ͣ������
һ��������εĶԳ��Ṳ____��.
5 ����������һ��������Ա��е���һ��ֱ�ߣ����ǶԳ��ᣬ����5���� �ʴ�Ϊ��5.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ� ��13�� ��Գ� ��Ԫ���Ծ� ���ͣ���ѡ��
��֪��ABC�У�AB��6��AC��8��BC��11������һ��ֱ�߽���ABC�ֳ����������Σ���������һ���������ǵ��������Σ���������ֱ������У� ��
A. 3�� B. 5�� C. 7�� D. 8��
C �������������������ͼ1����BC�Ĵ�ֱƽ���ߣ�DB=DC�� ��ͼ2����AB�Ĵ�ֱƽ���ߣ�DA=DB�� ��ͼ3����AC�Ĵ�ֱƽ���ߣ�DC=DA�� ��ͼ4����AΪԲ�ģ�ABΪ�뾶��Բ��AB=AD��AB=AE�� ��ͼ5����BΪԲ�ģ�BAΪ�뾶��Բ��BA=BD�� ��ͼ6����CΪԲ�ģ�CAΪ�뾶��Բ��CA=CD. ���Ͽ�֪��������ֱ�߹���7��. ��ѡC. ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��㶫ʡ���꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
���㣺��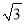 ��1��2+3tan30�㩁��
��1��2+3tan30�㩁��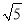 ��2����
��2����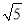 +2��+2sin60�㣮
+2��+2sin60�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��㶫ʡ���꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
�ڡ�����ТΪ�ȡ����б����У����������λ��ί������ijλ����ѡ�ֵķ������������±���
������ | ����λ�� | ƽ������ | ��� |
��8.5 | ��8.3 | ��8.1 | ��0.15 |
���ȥ��һ����߷ֺ�һ����ͷ֣���ô����������һ���������仯���ǣ�������
A. ƽ���� B. ��λ�� C. ���� D. ����
B �����������������ȥ��һ����߷ֺ�һ����ͷֶ���λ��û��Ӱ�죬 ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��5�� ͶӰ����ͼ ��Ԫ���Ծ� ���ͣ������
��ͼ�����ϣ�С�����ڴ���ϣ������֣�����վ�ڴ�����ߵ���յ·��֮�䣬�����Լ�������·�����ڵ��ϵ�����Ӱ�ӳ�һֱ��ʱ���Լ��ұߵ�Ӱ�ӳ�Ϊ3�ף���ߵ�Ӱ�ӳ�Ϊ1.5�ף���֪�Լ�����1.8�ף���յ·�Ƶĸ���ͬ����յ·��֮��ľ���Ϊ12�ף���·�Ƶĸ�Ϊ__________�ף�
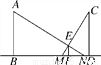
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����꼶��ѧ��ʦ����ϵڶ���ʵ��ר����Ծ� ���ͣ������
���㣺 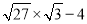 ��______.
��______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com