
��ͼ1��PΪ��MONƽ����OC��һ�㣬��PΪ����ġ�APB���߷ֱ�������OM��ON����A��B���㣬�����APB���Ƶ�P��תʱʼ������OA•OB=OP2 �� ���ǾͰѡ�APB������MON�Ĺ����ǣ�
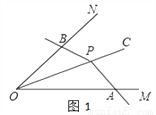
��1����ͼ2��PΪ��MONƽ����OC��һ�㣬��P��PB��ON��B��AP��OC��P����ô��APB________��MON�Ĺ����ǣ���ǡ����ǡ�����
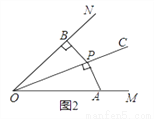
��2������ͼ3�������MON=60�㣬OP=2����APB�ǡ�MON�Ĺ����ǣ�����AB�����AOB������͡�APB�Ķ�����
�������MON=���㣨0�㣼���㣼90�㣩��OP=m����APB�ǡ�MON�Ĺ����ǣ�ֱ���ú��Ц���m�Ĵ���ʽ��ʾ��AOB�������
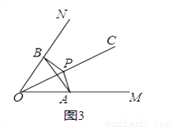
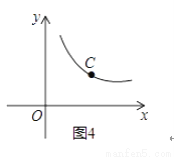
��3����ͼ4����C�Ǻ���y=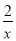 ��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ����ǡ�APB�Ķ���P�����꣮
��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ����ǡ�APB�Ķ���P�����꣮
 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018���п���ѧһ�ָ�ϰ��Ԫ��⣺��7�� һԪ���η��̣��飩��Ӧ�� ���ͣ������
��֪һԪ���η���x2��2x��1��0�������ֱ�Ϊx1��x2����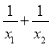 ��ֵΪ(����)
��ֵΪ(����)
A. 2 B. ��1
C. ��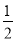 D. ��2
D. ��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ��������2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
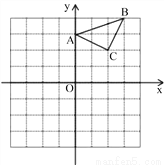
��֪����ABC������ƽ���ڣ��������������ΪA(0��3)��B(3��4)��C(2��2)��(�����������У�ÿ��С�����α߳�Ϊ1����λ����)
��1��������ABC����ƽ��4����λ�õ��ġ�A1B1C1��
��2����BΪλ�����ģ��������л�����A2BC2��ʹ��A2BC2���ABCλ�ƣ���λ�Ʊ�2��1��ֱ��д��C2�������� ��
��3����A2BC2������� ƽ����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ��������2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
һ�������ĺ�����װ��6����С��ͬ��ƹ��������4���ǻ���2���ǰ��Ӹú�������������һ������������ĸ�����(����)
A. 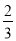 B.
B. 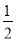 C.
C. 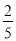 D.
D. 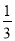
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018���п���ѧר�⸴ϰͬ����ϰ�⣺������Ǻ����ͽ�ֱ��������(�д�) ���ͣ������
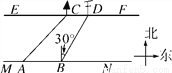
���ۺ�ʵ�����ϣ�С������С��Ҫ����һ���ӵĿ��ȣ���ͼ���Ӱ�EF��MN��С���ںӰ�MN�ϵ�A���ò�������úӶ�С��Cλ�ڶ�������Ȼ���غӰ�����30�ף�����B������úӶ����߸�Dλ�ڱ�ƫ��30�㷽��ʱ������ͬѧ���CD��10�ף���ӵĿ���Ϊ________��(�����������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ���һ ���ͣ������
������y=a��x��4��2��4��a��0����2��x��3��һ��λ��x����·�����6��x��7��һ��λ��x����Ϸ�����a��ֵΪ________��
1 �������������������������y=a��x-4��2-4��a��0���ĶԳ���Ϊֱ��x=4�� ����������6��x��7��һ��λ��x����Ϸ��� ����������1��x��2��һ��λ��x����Ϸ��� ����������2��x��3��һ��λ��x����·��� �������߹��㣨2��0���� �ѣ�2��0������y=a��x-4��2-4��a��0����4a-4=0�����a=1�� �ʴ�Ϊ��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ���һ ���ͣ������
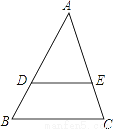
��ͼ���ڡ�ABC�У�DE��BC��AB=2BD����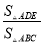 =________��
=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��29�� ͶӰ����ͼ ��Ԫ���� ���ͣ���ѡ��
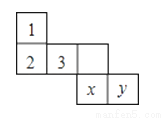
Ҫʹͼ��ƽ��չ��ͼ�������۵�����������������������֮��Ϊ6��x���ڣ�y���ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��㶫ʡ���꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
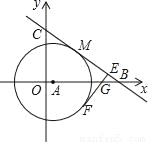
��ͼ����ƽ��ֱ������ϵ�У���֪��A��x�����ᣬ�Ե�AΪԲ������A����M��4��4���ڡ�A�ϣ�ֱ��y=��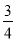 x+b��Բ�����ڵ�M���ֱ�x�ᡢy����B��C���㣮
x+b��Բ�����ڵ�M���ֱ�x�ᡢy����B��C���㣮
��1��ֱ��д��b��ֵ�͵�B�����ꣻ
��2�����A�������Բ�İ뾶��
��3����EF�С�A�ڵ�F�ֱ�AB��BC��G��E����FE��BC����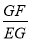 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com