练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线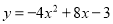的开口方向向______，对称轴是__________，最高点的坐标是_________，函数值得最大值是________。

    下 直线x=1 （1，1） 1 【解析】y=-4x2+8x-3=-4（x2-2x+1）+1=-4（x-1）2+1， ∴开口方向向下，对称轴是直线x=1，最高点的坐标是（1，1），函数值的最大值是1． 故答案为下；直线x=1；（1，1）；1．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    在平面直角坐标系中，点P（–2，x2+1）所在的象限是（ ）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    B 【解析】试题解析：∵x2≥0， ∴x2+1≥1， ∴点P（-2，x2+1）在第二象限． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型：填空题

    已知抛物线y=x2-2x-3关于原点对称的抛物线的解析式为____.

    y=-x2-2x+3. 【解析】试题分析：关于原点对称的两个二次函数，顶点坐标关于原点对称，开口方向改变．则原二次函数的解析式为： ，则对称后的解析式为： ．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：解答题

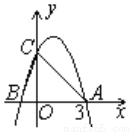
    如图所示，二次函数y=-x2+2x+m的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．

    （1）求m的值；

    （2）求点B的坐标；

    （3）该二次函数图象上有一点D（x，y）（其中x＞0，y＞0），使S△ABD=S△ABC，求点D的坐标．

    (1)m=3;(2)B（-1，0）（3）D（2，3）. 【解析】试题分析：（1）由二次函数y=﹣x2+2x+m的图象与x轴的一个交点为A（3，0），利用待定系数法将点A的坐标代入函数解析式即可求得m的值； （2）根据（1）求得二次函数的解析式，然后将y=0代入函数解析式，即可求得点B的坐标； （3）根据（2）中的函数解析式求得点C的坐标，由二次函数图象上有一点D（x，y）（其中x...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：填空题

    在平面直角坐标系中，若将抛物线y=2x2-4x+3先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是__________。

    （4，3） 【解析】抛物线y=2x2-4x+3=2(x2-2x+1)+1=2(x-1)2+1， 根据平移规律可得平移后解析式为y=2(x-1-3)2+1+2=2(x-4)2+3， 此时抛物线顶点坐标为（4,3）. 故答案为（4,3）.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：单选题

    在平面直角坐标系中，若将抛物线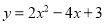先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后，所得到的抛物线的顶点坐标为（ ）

    A. （-2,3） B. （-1,4） C. （1,4） D. （4,3）

    D 【解析】坐标平移。 根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，将抛物线y=2x2 - 4x+3先向右平移3个单位长度，再向上平移2个单位长度，其顶点也同样变换。 ∵的顶点坐标是（1，1）， ∴点（1，1）先向右平移3个单位长度，再向上平移2个单位长度，得点（4，3），即经过这两次平移后所得抛物线的顶点坐标是（...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型：解答题

    如图，把一副三角板如图甲放置，其中∠ACB=DEC=90°，∠A=45°，∠D=30°，AB=6cm，DC=7cm．把三角板DCE绕点C顺时针旋转15°得到△D′CE′，如图乙，这时AB与CD′相交于点O，D′E′与AB、CB分别相交于点F、G，连接AD′．

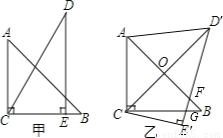
    （1）求∠OFE′的度数；

    （2）求线段AD′的长．

    （1）120°（2）5cm 【解析】 试题分析：（1）由∠BCE′=15°，∠E′=90°，易得∠CGE′=∠FGB=75°，可得∠OFE1=∠B+∠FGB=45°+75°=120°； （2）由∠OFE′=∠120°，得∠D′FO=60°，所以∠D′OF=90°，由AC=BC，AB=6cm，得OA=OB=OC=3cm，所以，OD′=CD′﹣OC=7﹣3=4cm，在Rt△AD′O中...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型：单选题

    如图，已知钝角三角形ABC，将△ABC绕点A按逆时针方向旋转110°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（　　）

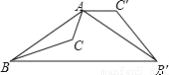
    A. 55° B. 65° C. 75° D. 85°

    C 【解析】分析：本题利用等腰三角形性质，旋转的性质和平行线的性质即可求出. 解析：由旋转知，AB=A B′,∠BA B′=110°,∴∠AB B′=∠A B′B=35° ，∵AC′∥BB′ ∴∠C′A B′=∠A B′B=35°，∴∠BAC=35°，∴∠CAB′=75°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（1）测试 题型：填空题

    如图，△ABC和△A′B′C是两个完全重合的直角三角板，∠B=30°，斜边长为10cm．三角板A′B′C绕直角顶点C顺时针旋转，当点A′落在AB边上时，CA′旋转所构成的扇形的弧长为______cm．

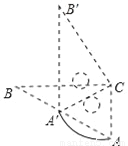
    【解析】试题解析：∵∠ACB=90°，∠B=30°，AB=16， ∴∠A=60°，AC=AB=5， ∵三角板A′B′C绕直角顶点C顺时针旋转，点A′落在AB边上， ∴CA′=CA， ∴△CAA′为等边三角形， ∴∠ACA′=60°， ∴弧AA′的长度=（cm）， 即点A′所转过的路径长cm．

    查看答案和解析>>

    同步练习册答案