
下列计算不正确的是( )
A. 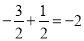 B.
B. 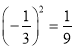 C.
C. 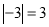 D.
D. 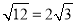
科目:初中数学 来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型:填空题
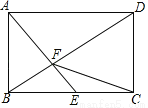
如图,在矩形ABCD中,AB=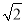 ,E是BC的中点,AE⊥BD于点F,则CF的长是_______.
,E是BC的中点,AE⊥BD于点F,则CF的长是_______.
查看答案和解析>>
科目:初中数学 来源:黑龙江省鸡西市虎林市八五八农场学校2018届九年级(上)期中考试数学试卷 题型:解答题
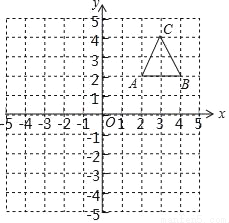
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
查看答案和解析>>
科目:初中数学 来源:黑龙江省鸡西市虎林市八五八农场学校2018届九年级(上)期中考试数学试卷 题型:填空题
原价100元的某商品,连续两次降价后售价为81元,若每次降低的百分率相同,则降低的百分率为 .
10%. 【解析】 试题解析:设这两次的百分率是x,根据题意列方程得 100×(1﹣x)2=81, 解得x1=0.1=10%,x2=1.9(不符合题意,舍去). 答:这两次的百分率是10%.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第1讲 实数概念与运算 题型:填空题
3的平方根是_________.
【解析】试题解析:∵( )2=3, ∴3的平方根是. 故答案为: .查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2018届九年级上学期期末考试数学试卷 题型:解答题
我市公共自行车项目现已建立了几百个站点,为人们的生活带来了方便.图  所示的是自行车的实物图
所示的是自行车的实物图 图
图 是一辆自行车的部分几何示意图,其中车架档AC的长为45cm,且
是一辆自行车的部分几何示意图,其中车架档AC的长为45cm,且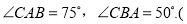
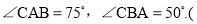 参考数据:
参考数据: 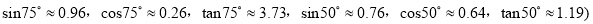

 求车座固定点C到车架档AB的距离;
求车座固定点C到车架档AB的距离;
 求车架档AB的长(第2小题结果精确到1cm).
求车架档AB的长(第2小题结果精确到1cm).
查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年八年级上学期期末数学试卷 题型:解答题
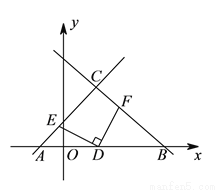
如图,在平面直角坐标系中,已知直线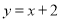 和
和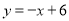 与
与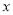 轴分别相交于点
轴分别相交于点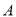 和点
和点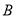 ,设两直线相交于点
,设两直线相交于点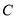 ,点
,点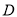 为
为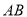 的中点,点
的中点,点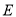 是线段
是线段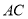 上一个动点(不与点
上一个动点(不与点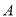 和
和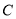 重合),连结
重合),连结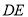 ,并过点
,并过点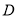 作
作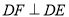 交
交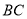 于点
于点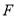 .
.
(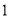 )判断
)判断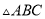 的形状,并说明理由.
的形状,并说明理由.
(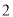 )当点
)当点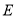 在线段
在线段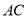 上运动时,四边形
上运动时,四边形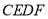 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
(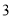 )当点
)当点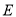 的横坐标为
的横坐标为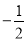 时,在
时,在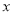 轴上找到一点
轴上找到一点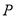 使得
使得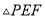 的周长最小,请直接写出点
的周长最小,请直接写出点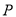 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年度上期期中测试八年级数学试卷 题型:单选题
如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
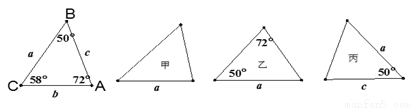
A. 甲 B. 乙与丙 C. 丙 D. 乙
B 【解析】乙图中利用角角边可证明全等. 丙图中可以用边角边可证明全等. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com