
дкЕШбќШ§НЧаЮABCжаЃЌ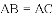
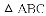
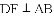
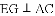
ЬюПеЃКЯпЖЮAFЃЌAGЃЌABжЎМфЕФЪ§СПЙиЯЕЪЧ______ЃЛ
ЯпЖЮMDЃЌMEжЎМфЕФЪ§СПЙиЯЕЪЧ______ЃЎ
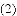
дкШЮвтШ§НЧаЮABCжаЃЌЗжБ№вдABКЭACЮЊаББпЯђ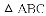
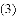
дкШЮвтШ§НЧаЮABCжаЃЌЗжБ№вдABКЭACЮЊаББпЃЌЯђ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2018ФъСЩФўЪЁНѕжнЪажаПМЪ§бЇЖўФЃЪдОэ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌе§ЗНаЮABCDжаЃЌ
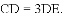
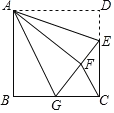
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁг§ВХбЇаЃ2018НьОХФъМЖжаПМЪ§бЇЖўеяЪдОэ ЬтаЭЃКНтД№Ьт
вбжЊЃКШчЭМ1ЃЌХзЮяЯп гыxжсНЛгк
гыxжсНЛгк






 ЃЌСЌНг
ЃЌСЌНг

 ШЁЕУзюаЁжЕЪБЃЌЧѓжБЯп
ШЁЕУзюаЁжЕЪБЃЌЧѓжБЯп


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁг§ВХбЇаЃ2018НьОХФъМЖжаПМЪ§бЇЖўеяЪдОэ ЬтаЭЃКЬюПеЬт
вђЪНЗжЁОНтЮіЁП ______ЃЎ
______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁг§ВХбЇаЃ2018НьОХФъМЖжаПМЪ§бЇЖўеяЪдОэ ЬтаЭЃКЕЅбЁЬт
ШчЭМЃЌЯТУцМИКЮЬхЕФИЉЪгЭМЪЧ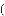

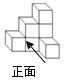
A. 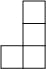 B.
B. 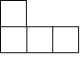 C.
C. 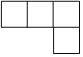 D.
D. 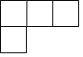
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃККгФЯЪЁхЇбєЪа2018НьОХФъМЖжаПМЪ§бЇЖўФЃЪдОэЃЈШЫНЬАцЃЉ ЬтаЭЃКНтД№Ьт
ЯШЛЏМђЃЌдйЧѓжЕЃКЃЈxЉ1Љ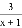 ЃЉЁТ
ЃЉЁТ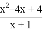 ЃЌШЛКѓДгТњзуЉ2ЃМxЁм2ЕФећЪ§жабЁдёвЛИіФуЯВЛЖЕФЪ§ДњШыЧѓжЕЃЎ
ЃЌШЛКѓДгТњзуЉ2ЃМxЁм2ЕФећЪ§жабЁдёвЛИіФуЯВЛЖЕФЪ§ДњШыЧѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃККгФЯЪЁхЇбєЪа2018НьОХФъМЖжаПМЪ§бЇЖўФЃЪдОэЃЈШЫНЬАцЃЉ ЬтаЭЃКЕЅбЁЬт
ШчЭМЃЌвЛЖЮХзЮяЯпЃК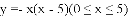
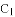 ЃЌЫќгыxжсНЛгкЕуOЃЌ
ЃЌЫќгыxжсНЛгкЕуOЃЌ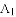 ЃЛНЋ
ЃЛНЋ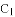 ШЦЕу
ШЦЕу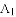 а§зЊ
а§зЊ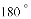 ЕУ
ЕУ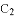 ЃЌНЛxжсгкЕу
ЃЌНЛxжсгкЕу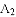 ЃЛНЋ
ЃЛНЋ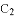 ШЦЕу
ШЦЕу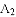 а§зЊ
а§зЊ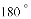 ЕУ
ЕУ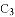 ЃЌНЛxжсгкЕу
ЃЌНЛxжсгкЕу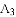 ЃЛ
ЃЛ
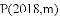
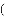

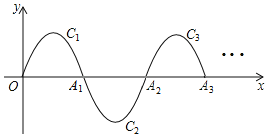
A. 4 B. 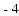
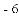
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2018 ГѕШ§Ъ§бЇжаПМзмИДЯА ВЛЕШЪН(зщ)МАЦфгІгУ зЈЬтбЕСЗЬт КЌД№АИ ЬтаЭЃКЬюПеЬт
ВЛЕШЪНзщ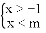 га3ИіећЪ§НтЃЌдђmЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
га3ИіећЪ§НтЃЌдђmЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКШЫНЬАцАЫФъМЖЯТВс ЕкЪЎОХеТЁЖвЛДЮКЏЪ§злКЯгІгУЁЗЬсИпМьВтЪдОэ ЬтаЭЃКНтД№Ьт
вЛДЮКЏЪ§ ЃЌгы
ЃЌгы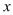 жсЁЂ
жсЁЂ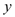 жсНЛЕуЗжБ№ЮЊ
жсНЛЕуЗжБ№ЮЊ ЁЂ
ЁЂ ЃЌШє
ЃЌШє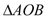 ЕФжмГЄЮЊ
ЕФжмГЄЮЊ ЃЈ
ЃЈ ЮЊзјБъдЕуЃЉЃЌЧѓ
ЮЊзјБъдЕуЃЉЃЌЧѓ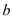 ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com