
如图,第(1)个图案中有4个等边三角形,第(2)个图案中有7个等边三角形,第(3)个图案中有10个等边三角形,……,以此规律,第n个图案中有____________个等边三角形(用含n的代数式表示).

科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:单选题
下列说法不正确的是( )
A. 方程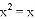 有一根为0
有一根为0
B. 方程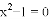 的两根互为相反数
的两根互为相反数
C. 方程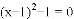 的两根互为相反数
的两根互为相反数
D. 方程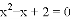 无实数根
无实数根
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
已知: 如图,⊙O的直径AB的长为5cm,C为⊙O上的一个点,∠ACB的平分线交⊙O于点D,求BD的长.

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:单选题
在半径为12cm的圆中,长为 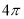 cm的弧所对的圆心角的度数为
cm的弧所对的圆心角的度数为
A. 10° B. 60° C. 90° D. 120°
B 【解析】设4πcm的弧所对的圆心角的度数为n°,由题意得 , ∴n=60° 故选B.查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
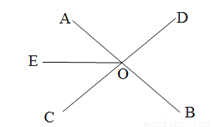
如图,直线AB、CD相交于点O,OE平分∠AOC,∠BOC-∠BOD = 20°,求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
已知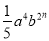 与
与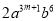 是同类项,则
是同类项,则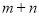 =____________.
=____________.
查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
某班分两组去两处植树,第一组22人,第二组26人,现在第一组植树遇到困难,需第二组支援,问从第二组调多少人去第一组才能使第一组人数是第二组的2倍,设抽调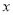 人,则可列方程为( )
人,则可列方程为( )
A. 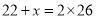 B.
B. 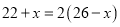
C. 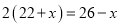 D.
D. 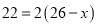
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
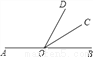
如图,点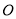 在直线
在直线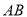 上,射线
上,射线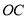 平分
平分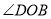 ,若
,若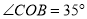 ,则
,则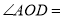 __度.
__度.
查看答案和解析>>
科目:初中数学 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com