练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知： 如图，⊙O的直径AB的长为5cm，C为⊙O上的一个点，∠ACB的平分线交⊙O于点D，求BD的长．

    【解析】试题分析：根据圆周角定理及角平分线的性质，可得∠ADB=90°、AD=BD；再利用等腰直角三角形的性质及解直角三角形的知识，即可得到BD的长. 解：∵ AB为直径， ∴ ∠ADB=90°， ∵ CD平分∠ACB， ∴ ∠ACD=∠BCD， ∴=． ∴ AD=BD 在等腰直角三角形ADB中， BD=ABsin45°=5×= ∴ BD=. ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    若点P（a+1,2a-3）关于x轴的对称点在第一象限内，则a的取值范围是________________

    -1

    查看答案和解析>>

    科目：初中数学 来源：北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型：解答题

    点P（1，4），Q（2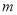， ）是双曲线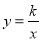图象上一点．

    （1）求k值和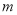值．

    （2）O为坐标原点．过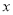轴上的动点R作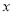轴的垂线，交双曲线于点S，交直线OQ于点T，且点S在点T的上方．结合函数图象，直接写出R的横坐标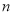的取值范围．

    （1）， ；（2） 或． 【解析】试题分析：（1）把点P（1，4）代入得k=4；把Q（2， ）代入得m=2; （2）作出图象，容易得出结论. 试题解析：（1）点P（1，4），Q（2， ）是双曲线图象上一点． ， ， （2）如图所示， ∴ 或

    查看答案和解析>>

    科目：初中数学 来源：北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型：单选题

    如图，Rt△ABC中，∠C=90°，AC=4，BC=3．以点A为圆心，AC长为半径作圆．则下列结论正确的是（ ）

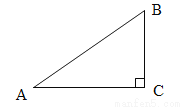
    A. 点B在圆内 B. 点B在圆上

    C. 点B在圆外 D. 点B和圆的位置关系不确定

    C 【解析】试题解析：如图， ∵在Rt△ABC中，∠C=90°，AC=4，BC=3， ∴AB=． ∵AB=5＞4， ∴点B在⊙A外． 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京大兴区2017-2018学年度第一学期期末检测试卷 题型：解答题

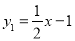    已知一次函数，二次函数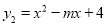（其中m＞4）．

    （1）求二次函数图象的顶点坐标（用含m的代数式表示）；

    （2）利用函数图象解决下列问题：

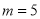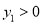    ①若，求当且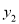≤0时，自变量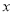的取值范围；

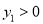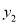    ②如果满足且≤0时自变量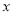的取值范围内有且只有一个整数，直接写出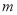的取值范围．

    （1）；（2）①2＜x≤4．②≤m＜5. 【解析】试题分析：（1）把y2=x2-mx+4通过配方转化成顶点式即可求得顶点坐标． （2）①当m=5时，y2=x2-5x+4，画出函数的图象，根据图象即可求得自变量x的取值范围； ②根据题意结合图象可知x=3，把x=3代入y2=x2-mx+4≥0即可求得a的取值； 【解析】 （1）∵， ∴二次函数图象的顶点坐标为 . ...

    查看答案和解析>>

    科目：初中数学 来源：北京大兴区2017-2018学年度第一学期期末检测试卷 题型：填空题

    下面是“作出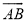所在的圆”的尺规作图过程．

    已知： ．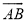

    求作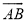： 所在的圆.

    作法：如图，

    (1)在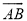上任取三个点D，C，E；

    (2)连接DC，EC；

    （3）分别作DC和EC的垂直平分线， 两垂直平分线的交点为点O.

    （4）以 O为圆心，OC长为半径作圆，所以⊙O即为所求作的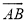所在的圆..

    请回答：该尺规作图的依据是____．

    不在同一直线上的三个点确定一个圆；圆是到定点的距离等于定长的点的集合；线段垂直平分线上的点到线段两个端点的距离相等. 【解析】该尺规作图的依据是：不在同一直线上的三个点确定一个圆；圆是到定点的距离等于定长的点的集合；线段垂直平分线上的点到线段两个端点的距离相等.

    查看答案和解析>>

    科目：初中数学 来源：北京大兴区2017-2018学年度第一学期期末检测试卷 题型：填空题

    如图，在Rt△ABC中，∠C＝90°，BC＝4，AC=2，则tanB的值是__________．

    【解析】.

    查看答案和解析>>

    科目：初中数学 来源：湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    如图，第（1）个图案中有4个等边三角形，第（2）个图案中有7个等边三角形，第（3）个图案中有10个等边三角形，……，以此规律，第n个图案中有____________个等边三角形（用含n的代数式表示）．

    3n+1 【解析】第一个图案中等边三角形的个数：4=3+1； 第二个图案中等边三角形的个数：7=3×2+1； 第三个图案中等边三角形的个数：10=3×3+1； … ∴第n个图案中等边三角形的个数就应该为：（3n+1）， 故答案为：（3n+1）．

    查看答案和解析>>

    科目：初中数学 来源：北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型：解答题

    为发展校园足球运动，某城区四校决定联合购买一批足球运动装备.市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折.

    （1）求每套队服和每个足球的价格是多少元；

    （2）若城区四校联合购买100套队服和a（a＞10）个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花发费用；

    （3）在（2）的条件下，若a=60，假如你是本次购买任务的负责人，你认为到甲、乙哪家商场购买比较合算？

    （1）每套队服150元，每个足球100元；（2）甲：（100a+14000）元，乙：（80a+15000)元；（3）在乙商场购买比较合算. 【解析】试题分析：（1）设每个足球的定价是x元，则每套队服是（x+50）元，根据两套队服与三个足球的费用相等列出方程，解方程即可； （2）根据甲、乙两商场的优惠方案列式即可； （3）把a=60分别代入（2）中求得的代数式计算后进行比较即可得．...

    查看答案和解析>>

    同步练习册答案