
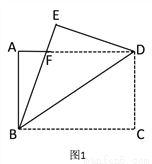
��ͼ 1����һ�ž���ֽƬ ABCD ���ŶԽ��� BD �����۵������� C �䵽�� E ����BE �� AD �ڵ� F.
��1����֤����BDF �ǵ��������Σ�
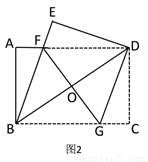
��2����ͼ 2������ D �� DG��BE���� BC �ڵ� G������ FG �� BD �ڵ� O.
���ж��ı��� BFDG ����״����˵�����ɣ�
���� AB=6��AD=8���� FG �ij�Ϊ_____.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ڶ�ѧ�������л�ɽ����һ��ѧ��ĩ�Ծ� ���ͣ������
��1���ⷽ���飺  ����2����ʽ
����2����ʽ ����������⣮
����������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ������2017-2018ѧ�����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
m��n��������������ʽxm+xn+3xm+n�Ĵ����ǣ�������
A. 2m+2n B. m��n C. m+n D. m��n�еĽϴ���
C ����������m��n���������� ��m+n>m��m+n>n�� ��m+n��� �����ʽxm+xn+3xm+n�Ĵ�����m+n�� ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ��ζ�����һѧ�ھ��꼶����ѧҵ�������в��ԣ�2018�����һģ�� ���ͣ������
�����ABC�ס�DEF���Ҷ�Ӧ���֮��Ϊ1��4����ô���Ƕ�Ӧ�ܳ�֮��Ϊ_____��
1��2�� ������������������ߡ�ABC�ס�DEF�������Ϊ1��4�� ���ABC���DEF�����Ʊ�Ϊ1��2�� ���ABC���DEF�Ķ�Ӧ�ܳ�֮��Ϊ1��2�� �ʴ�Ϊ1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ��ζ�����һѧ�ھ��꼶����ѧҵ�������в��ԣ�2018�����һģ�� ���ͣ���ѡ��
��֪����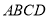 �ĶԽ���
�ĶԽ���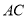 ��
��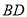 �ཻ�ڵ�
�ཻ�ڵ�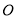 �����
�����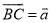 ��
�� 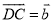 ����ô
����ô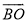 ����( )
����( )
A. 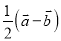 �� B.
�� B. 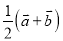 �� C.
�� C. 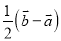 �� D.
�� D. 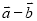 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ������
��ͼΪij���в��ֵֽ�ʾ��ͼ,�ı���ABCDΪ������,��G�ڶԽ���BD��,GE��CD,GF��BC,AD=1 500 m,С�����ߵ�·��ΪB��A��G��E,С�����ߵ�·��ΪB��A��D��E��F.��С�����ߵ�·��Ϊ3 100 m,��С�����ߵ�·��Ϊ �� m.
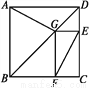
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ���ѡ��
�á����巨����÷��̣�2x+5��2-4(2x+5)+3=0�Ľ�Ϊ�� ��
A. x1=1 x2=3 B. x1=-2 x2=3 C. x1=-3 x2=-1 D. x1=-2 x2=-1
D ���������������� ��2x+5��2��4��2x+5��+3=0����2x+5=y����ԭ���̱���Ϊy2��4y+3=0����ã�y1=1��y2=3����y=1ʱ��2x+5=1����ã�x=��2����y=3ʱ��2x+5=3����ã�x=��1����ԭ���̵Ľ�Ϊx1=��2��x2=��1����ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���˽̰���꼶��ѧ�²���в��� ���ͣ������
�ҹ��Ŵ�������һ����ѧ����:����ľһ��ֱ������,�߶���,������,�и����Ը����ƶ���,���ܶ����䶥,�ʸ���֮������?��������:��ͼ��ʾ,�ѿ�ľ����һ��Բ����,��һ����ʮ��,���Բ���ĸ�Ϊ20��,�����ܳ�Ϊ3��,�и����Ե�A�����ƶ���,�����ܺ���ĩ��ǡ�õ����B��,�������и��ٵ���̳����� ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ�⣨������ͼ�ۼ�����д������
��ͼ��A��B������һ��С��MN��ͬһ�࣬Ҫ�ںӱ߽�һˮ�������幩ˮ��
��1����Ҫʹ����ˮ��������ľ�����ȣ���ַPӦѡ���ĸ�λ�ã�
��2����Ҫʹ����ˮ�����������ˮ��������ʡ����ַQӦѡ���ĸ�λ�ã�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com