
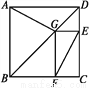
��ͼΪij���в��ֵֽ�ʾ��ͼ,�ı���ABCDΪ������,��G�ڶԽ���BD��,GE��CD,GF��BC,AD=1 500 m,С�����ߵ�·��ΪB��A��G��E,С�����ߵ�·��ΪB��A��D��E��F.��С�����ߵ�·��Ϊ3 100 m,��С�����ߵ�·��Ϊ �� m.
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ڶ�ѧ�������л�ɽ����һ��ѧ��ĩ�Ծ� ���ͣ������
������ʽ ��һ����ȫƽ��ʽ����
��һ����ȫƽ��ʽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ��ζ�����һѧ�ھ��꼶����ѧҵ�������в��ԣ�2018�����һģ�� ���ͣ������
��֪��ƽ��ֱ������ϵxOy����ͼ���У���֪������y=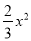 +bx+c�㾭��A��1��0����B��0��2����
+bx+c�㾭��A��1��0����B��0��2����
��1����������ߵı���ʽ��
��2����������ߵĶԳ�����x��Ľ���ΪC�����������ڵĵ�D�ڸ������ߵĶԳ����ϣ�����Ե�A��C��D����ɵ����������AOB���ƣ����D�����ꣻ
��3�����E�ڸ������ߵĶԳ����ϣ�������������1������AE��BE����sin��ABE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ��ζ�����һѧ�ھ��꼶����ѧҵ�������в��ԣ�2018�����һģ�� ���ͣ������
��֪��P���߶�AB�ϣ���AP��BP=2��3����ôAB��PB=_____��
5��3�� �����������������������AP��BP=2��3�� AB��PB=��AP+PB����PB=��2+3����3=5��3. �ʴ�Ϊ��5:3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ������
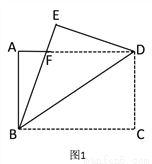
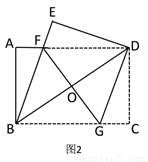
��ͼ 1����һ�ž���ֽƬ ABCD ���ŶԽ��� BD �����۵������� C �䵽�� E ����BE �� AD �ڵ� F.
��1����֤����BDF �ǵ��������Σ�
��2����ͼ 2������ D �� DG��BE���� BC �ڵ� G������ FG �� BD �ڵ� O.
���ж��ı��� BFDG ����״����˵�����ɣ�
���� AB=6��AD=8���� FG �ij�Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ������
����x2=4x�Ľ� __��
x=0��x=4 ����������������������ʹ�����ұ�Ϊ0�����ṫ��ʽx��Ȼ����ݡ���ʽ���ֵΪ0������ʽ��������һʽֵΪ0����������⣮ �������� ԭ���̱�Ϊ x2��4x=0 x��x��4��=0 ���x1=0��x2=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ���ѡ��
����x��һԪ���η���x2+��m��2��x+m+1=0��������ȵ�ʵ��������m��ֵ�ǣ�������
A. 0 B. 8 C. 4��2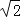 D. 0��8
D. 0��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���˽̰���꼶��ѧ�²���в��� ���ͣ������
��ͼ��?ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AE��BC������ΪE��AB= ��AC=2��BD=4����AE�ij�Ϊ( ��)
��AC=2��BD=4����AE�ij�Ϊ( ��)

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
һ�����������ε�һ���ڽ��� ������������εĵ�Ϊ___________
������������εĵ�Ϊ___________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com