
(1)解方程组:  ;(2)求不等式
;(2)求不等式 的最大整数解.
的最大整数解.
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:解答题
已知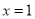 是关于x的方程
是关于x的方程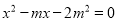 的一个根,求
的一个根,求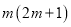 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:云南省2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
某街道改建工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书,从投标书中得知,若由甲队先做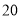 天可完成总工程的
天可完成总工程的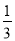 ,剩下的工程再由甲、乙两队合作
,剩下的工程再由甲、乙两队合作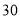 天可以完成.
天可以完成.
(1)求乙队单独完成这项工程需多少天?
(2)已知甲队每天的施工费用为0.8万元,乙队每天的施工费用为0.4万元,工程预算的施工费用为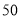 万元,为缩短工期以减少对住户的影响,拟安排甲、乙两个工程队合作完成这项工程,则工程预算的费用是否够用?若不够用,需追加预算费用多少万元?请给出你的判断并说明理由.
万元,为缩短工期以减少对住户的影响,拟安排甲、乙两个工程队合作完成这项工程,则工程预算的费用是否够用?若不够用,需追加预算费用多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源:云南省2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
下列多项式中,完全平方式有( )个
a2-4a+4,1+4a2,4b2+4b-1,a2+ab+b2
A. 1个 B. 2个 C. 3个 D. 4个
A 【解析】a2-4a+4=(a-2)2,所以选A.查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:解答题
9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从无锡出发,1日到4日在北京旅游,8月5日上午返回无锡.
无锡与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:

假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)若去时坐火车,回来坐飞机,且飞机成人票打五五折,其他开支不变,他们准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
(1);(2)标准间房价每日每间不能超过450元. 【解析】试题分析:(1)结合梯次旅游总共开支了13668元,以及他们四个人在北京的住宿费刚好等于表中所示其他三项费用之和分别得出等式,列出方程组,解得答案即可; (2)结合他们往返都坐飞机(成人票五五折),求出总费用,进而求出答案. 试题解析:(1)往返高铁费:(524×3+524÷2)×2=3668元 解得: ; ...查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:填空题
若多项式 是一个完全平方式,则
是一个完全平方式,则
查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:单选题
若关于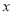 的不等式组
的不等式组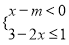 的所有整数解的和是10,则m的取值范围是( )
的所有整数解的和是10,则m的取值范围是( )
A. 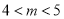 B.
B. 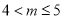 C.
C. 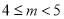 D.
D. 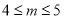
查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:解答题
15-[3+(-5-4)]
21 【解析】试题分析:有理数的加减混合运算,如果带有括号,按照小括号、中括号的顺序进行计算即可. 试题解析:15-[3+(-5-4)]=15-(3-9)=15-(-6)=15+6=21.查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:解答题
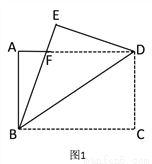
如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE 交 AD 于点 F.
(1)求证:△BDF 是等腰三角形;
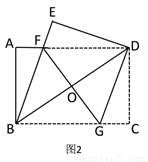
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;
②若 AB=6,AD=8,则 FG 的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com