练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    函数中自变量的取值范围是______________

    x≤2且x≠1 【解析】试题解析：根据题意得：且x?1≠0， 解得：且 故答案为：且
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年广东省河源市中考数学一诊试卷 题型：单选题

    正八边形的每个内角为 (　　)

    A. 120° B. 135° C. 140° D. 144°

    B 【解析】试题分析：根据正多边形的内角求法，得出每个内角的表示方法，即可得出答案． 【解析】 根据正八边形的内角公式得出：[（n﹣2）×180]÷n=[（8﹣2）×180]÷8=135°． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    已知二次函数y=x2-2x-3.

    （1）求出这个函数图象的对称轴和顶点坐标：

    （2）求出这个函数图象与x轴、y轴的交点坐标.

    （1）对称轴是x=1，顶点坐标是（1，-4）； （2）图象与x轴交点坐标是（-l，0）、（3，0），与y轴的交点坐标是（0，-3） 【解析】试题分析：（1）利用配方法整理到顶点式即可得； （2）分别令x=0、y=0，解方程即可得. 试题解析：（1）∵y=x2-2x-3=（x-1）2-4， ∴对称轴是x=1，顶点坐标是（1，-4）； （2）令y=0，则x2-2x-...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题

    如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11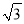， ≈1.73）

    13米． 【解析】试题分析：根据矩形性质得出DG=CH，CG=DH，再利用锐角三角函数的性质求出问题即可． 试题解析：如图，过点D作DG⊥BC于G，DH⊥CE于H， 则四边形DHCG为矩形． 故DG=CH，CG=DH， 在直角三角形AHD中， ∵∠DAH=30°，AD=6， ∴DH=3，AH=3， ∴CG=3， 设BC为x， 在直角三角形...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：填空题

    在临桂新区建设中，需要修一段全长2400m的道路，为了尽量减少施工对县城交通工具所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度．若设原计划每天修路xm，则根据题意可得方程　 　．

    8. 【解析】试题解析：∵原计划用的时间为： 实际用的时间为： ∴可列方程为： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：单选题

    如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

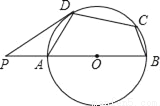
    A. 40° B. 35° C. 30° D. 45°

    C 【解析】试题分析：连接BD，∵∠DAB=180°﹣∠C=60°，∵AB是直径，∴∠ADB=90°，∴∠ABD=90°﹣∠DAB=30°，∵PD是切线，∴∠ADP=∠ABD=30°，故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：解答题

    如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.

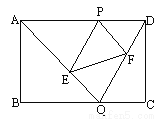
    （1）求证：△APE∽△ADQ；

    （2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？

    （3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）

    （1）证∠APE=∠ADQ，∠AEP=∠AQD. 注意到△APE∽△ADQ与△PDE∽△ADQ，及S△PEF=， 得S△PEF==. ∴当，即P是AD的中点时，S△PEF取得最大值. （3）作A关于直线BC的对称点A′，连DA′交BC于Q，则这个点Q就是使△ADQ周长最小的点，此时Q是BC的中点. 【解析】（1）证得∠APE=∠ADQ，∠AEP=∠AQD，即可得到△APE∽...

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：单选题

    如果圆锥的母线长为6cm，底面圆半径为3cm，则这个圆锥的侧面积为（　　）

    A. 9πcm2 B. 18πcm2 C. 27πcm2 D. 36πcm2

    B 【解析】底面圆半径为3cm，则底面周长=6π，圆锥的侧面积=×6π×6=18πcm2． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：填空题

    如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是_____cm．

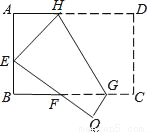
    8 【解析】试题分析：BE=AB-AE=2.设AH=x，则DH=AD﹣AH=8﹣x，在Rt△AEH中，∠EAH=90°，AE=4，AH=x，EH=DH=8﹣x，∴EH2=AE2+AH2，即（8﹣x）2=42+x2，解得：x=3．∴AH=3，EH=5.∴C△AEH=12.∵∠BFE+∠BEF=90°，∠BEF+∠AEH=90°，∴∠BFE=∠AEH．又∵∠EAH=∠FBE=90°，∴△EBF∽...

    查看答案和解析>>

    同步练习册答案