
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
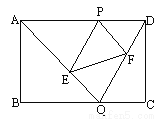
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
(1)证∠APE=∠ADQ,∠AEP=∠AQD. 注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=, 得S△PEF==. ∴当,即P是AD的中点时,S△PEF取得最大值. (3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点. 【解析】(1)证得∠APE=∠ADQ,∠AEP=∠AQD,即可得到△APE∽...科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
已知关于 的方程
的方程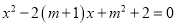 .
.
(1)若方程总有两个实数根,求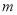 的取值范围;
的取值范围;
(2)若两实数根 、
、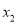 满足
满足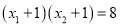 ,求
,求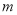 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:单选题
二次函数y=(x+1)2-2的最小值是( ).
A. 1 B. -1 C. 2 D. -2
D 【解析】试题分析:根据二次函数的性质,当时,二次函数的最小值为-2.故选D.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:填空题
函数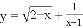 中自变量的取值范围是______________
中自变量的取值范围是______________
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
下列命题中的假命题是( )
A. 一组邻边相等的平行四边形是菱形
B. 一组邻边相等的矩形是正方形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等且有一个角是直角的四边形是矩形
D 【解析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项. 【解析】 A、根据菱形的判定定理,正确; B、根据正方形和矩形的定义,正确; C、符合平行四边形的定义,正确; D、错误,可为不规则四边形. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:解答题
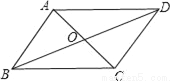
(1)如图,在□ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
(2)规定:一条弧所对的圆心角的度数作为这条弧的度数.
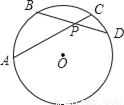
①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,求∠APB;
②一般地,在⊙O中,弦AC、BD相交于点P,若弧AB、弧CD分别为m°和n°,求∠APB.
(用m、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:填空题
一粒纽扣式电池能够污染60升水,太原市每年报废的电池有近10000000粒,如果废旧电池不回收,一年报废的电池所污染的水约_____升(用科学记数法表示).
6×108升 【解析】60×10 000 000=600 000 000=6×108查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:解答题
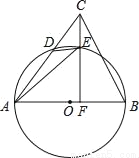
如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在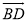 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4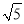 ,cos∠ACF=
,cos∠ACF=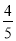 ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:单选题
若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A. 矩形 B. 菱形
C. 对角线相等的四边形 D. 对角线互相垂直的四边形
D 【解析】由于E、F、G、H分别是AB、BC、CD、AD的中点, 根据三角形中位线定理得:EH ∥ FG ∥ BD,EF ∥ AC ∥ HG; ∵四边形EFGH是矩形,即EF⊥FG, ∴AC⊥BD,即对角线互相垂直, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com