
从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( )
A. 9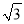 B. 9(
B. 9(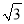 -1) C. 9(
-1) C. 9(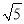 -1) D. 9
-1) D. 9
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
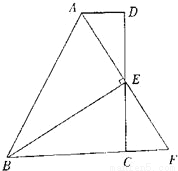
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源:安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
本学期我县义务教育阶段在校学生人数约为13.5万,数13.5万用科学计数法表示为( )
(A) 13.5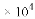 (B) 1.35
(B) 1.35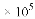 (C) 0.135
(C) 0.135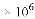 (D) 135
(D) 135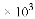
查看答案和解析>>
科目:初中数学 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:单选题
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
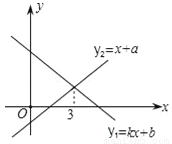
A. 0 B. 1 C. 2 D. 3
B 【解析】试题分析:∵y1=kx+b的函数值随x的增大而减小,∴k<0;故①正确 ∵y2=x+a的图象与y轴交于负半轴,∴a<0; 当x<3时,相应的x的值,y1图象均高于y2的图象, ∴y1>y2,故②③错误.查看答案和解析>>
科目:初中数学 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:单选题
关于的一次函数y=kx+k2+1的图象可能是( )
A. 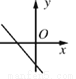 B.
B. 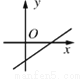 C.
C. 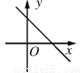 D.
D. 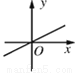
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
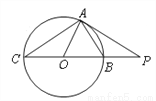
如图,PA为⊙O的切线,A为切点.直线PO与⊙O交于B,C两点,∠P=30°,连接AO,AB,AC.求证:ΔACB≌ΔAPO.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
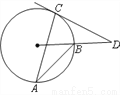
如图AB,AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:单选题
如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )

A. 40° B. 45° C. 50° D. 55°
A 【解析】试题分析:首先利用三角形内角和定理求得∠BAC的度数,然后利用角平分线的性质求得∠CAD的度数即可. 【解析】 ∵∠B=67°,∠C=33°, ∴∠BAC=180°﹣∠B﹣∠C=180°﹣67°﹣33°=80° ∵AD是△ABC的角平分线, ∴∠CAD=∠BAC=×80°=40° 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )
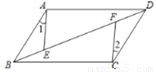
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
C 【解析】试题分析:因为四边形ABCD是平行四边形,所以AB//CD,AB=CD,所以∠ABD=∠CDB,所以要使△ABE≌△CDF, 若添加条件:∠1=∠2,可以利用ASA证明△ABE≌△CDF,所以D正确,若添加条件:BE=FD,可以利用SAS证明△ABE≌△CDF,所以B正确,若添加条件:BF=DE,可以得到BE=FD,可以利用SAS证明△ABE≌△CDF,所以C正确;若添加条...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com