
��ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
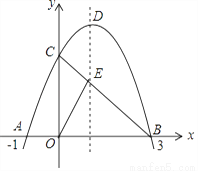
��1����������ߵĽ���ʽ��
��2��ֱ��д����C�͵�D�����ꣻ
��3������P�ڵ�һ�����ڵ��������ϣ���S��ABP=4S��COE �� ��P�����꣮
��1��y=-x2+2x+3��2��D��1��4����3��P��2��3�� �������������������1����A��B��������������ߵĽ���ʽ�У������������ϵ��b��c��ֵ�������ɵõ������ߵĶԳ��᷽�̣� ��2����x=0���ɵ�C�����꣬����������ʽ�䷽���������ߵĶ���C�����ꣻ ��3����P��x��y����x��0��y��0�������������г����̼������y������D�����꣮ ��1���ɵ�A����1��0���͵�B��3...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�人�н�����2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��֪����������y= 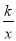 ��ͼ����P����1��2���������������ͼ��λ�ڣ� ��
��ͼ����P����1��2���������������ͼ��λ�ڣ� ��
A. ��һ�������� B. �ڶ��������� C. �ڶ��������� D. ������������
C ������������������y= ��ͼ����P����1��2���� ��2= �� ��k=��2��0�� �ຯ����ͼ��λ�ڵڶ��������ޣ� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
�������ڽǷֱ������ǶԽǵ�һ����ı��ν�����Խ��ı��Σ�
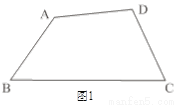
��1����ͼ1���ڰ�Խ��ı���ABCD�У���B��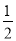 ��D����C��
��D����C��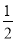 ��A�����B���C�Ķ���֮�ͣ�
��A�����B���C�Ķ���֮�ͣ�
��2����ͼ2����ǡ�ABC�ڽ��ڡ�O������AB�ϴ���һ��D��ʹ��BD��BO����OBA��ƽ���߽�OA�ڵ�E������DE���ӳ���AC�ڵ�F����AFE��2��EAF��
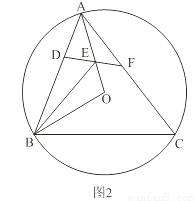
��֤���ı���DBCF�ǰ�Խ��ı��Σ�
��3����ͼ3���ڣ�2���������£�����D��DG��OB�ڵ�H����BC�ڵ�G����DH��BGʱ�����BGH���ABC�����֮�ȣ�
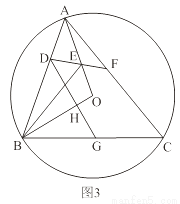
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ������ֽƬABCD�У�AB=4��BC=8����ֽƬ�۵���ʹ��C���A�غϣ��ۺ�ΪEF����D�Ķ�Ӧ��ΪG������DG����ͼ����Ӱ��������ǣ� ��
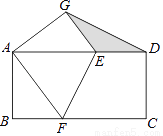
A. 5 B. 3 C. 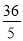 D.
D. 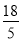
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж�Ǯ����У2018����꼶�ϲ�����������ѧ�Ծ� ���ͣ������
��2016�㽭ʡ�����У��������Σ����ǵ��������Σ�һ����������һ�������ڶԱ��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
��1����ͼ1���ڡ�ABC�У�CDΪ��ƽ���ߣ���A=40�㣬��B=60�㣬��֤��CDΪ��ABC�������ָ��ߣ�
��2���ڡ�ABC�У���A=48�㣬CD�ǡ�ABC�������ָ��ߣ��ҡ�ACDΪ���������Σ����ACB�Ķ�����
��3����ͼ2����ABC�У�AC=2��BC=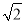 ��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
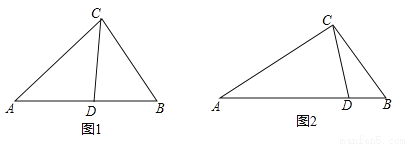
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж�Ǯ����У2018����꼶�ϲ�����������ѧ�Ծ� ���ͣ������
��һ�������Ŀڴ��У�װ�����ɸ�����ɫ��ͬ�⣬�����ͬ��С������ڴ���װ��3�������Ҵ����������һ�����Ǻ���ĸ���Ϊ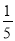 ����ô�ڴ���С����_____����
����ô�ڴ���С����_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж�Ǯ����У2018����꼶�ϲ�����������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����D��0��3����O��0��0����C��4��0���ڡ�A�ϣ�BD�ǡ�A��һ���ң���sin��OBD=��������
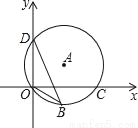
A. 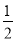 B.
B. 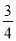 C.
C. 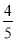 D.
D. 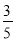
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����У�����У���� 2017-2018ѧ����꼶��һѧ�����в�����ѧ�Ծ� ���ͣ���ѡ��
����˵����ȷ����(�� ��)
A. ��Ӧ�߶��ɱ����Ķ�������� B. ��Ӧ�Ƕ���ȵĶ��������
C. ������ͬ������������� D. ���ζ�����
C �������������������������ͼ�εĶ��壬��ѡ��һһ�������ų�����𰸣� �������� A����Ӧ�߶��ɱ����Ķ���Σ�������״��Ψһȷ����ͼ�Σ��ʴ��� B����Ӧ�Ƕ���ȵĶ���Σ�������״��Ψһȷ����ͼ�Σ��ʴ��� C��������ͬ��������Σ���״��ͬ������С��һ����ͬ������ȷ�� D������������״��Ψһȷ����ͼ�Σ��ʴ��� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ�����꼶��ѧ�²� ��ĩ���� ���ͣ������
һ�κ���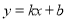 ��
��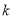 ��
�� 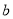 ������
Ϊ������ 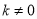 ����ͼ����ͼ��ʾ������ͼ����Ϣ����ù���
����ͼ����ͼ��ʾ������ͼ����Ϣ����ù���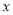 �ķ���
�ķ���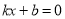 �Ľ�Ϊ__________��
�Ľ�Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com