
ֱ��y=m��ƽ����X���ֱ�ߣ���������y=��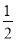 x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������У2017-2018ѧ�����꼶��ѧ�ڵڶ��ο�����ѧ�Ծ� ���ͣ������
����ʽ ��ϵ����__________,������__________.
��ϵ����__________,������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ������
��֪С���ﳵ�Ͳ��е��ٶȷֱ�Ϊ240��/�֣�80��/�֣�С��ÿ�δӼҲ��е�ѧУ����ʱ����ͬ���������С���С���ĶԻ�����(��ͼ)����С���Ӽҵ�ѧУ��·�̺�С��ӼҲ��е�ѧУ�����ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ���ѡ��
��ͼ������·����һ��ׯO����Ҫ��һ��վ��Ϊ��ʹ��ׯ�˳˳���㣬��������·����ѡһ��������վ��Ӧ����(�� ��)
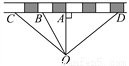
A. A�� B. B�� C. C�� D. D��
A ��������������������ݴ��߶���̿ɵã�Ӧ����A���� ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�к�ɽ��2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ�����κ���y=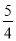 x2��0��x��2����ͼ���Ϊ����C1����C1������ԭ��O��ʱ����ת90�㣬������C2
x2��0��x��2����ͼ���Ϊ����C1����C1������ԭ��O��ʱ����ת90�㣬������C2
��1���뻭��C2��
��2��д����ת��A��2��5���Ķ�Ӧ��A1�����ꣻ
��3��ֱ��д��C1��ת��C2������ɨ���������
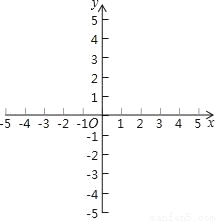
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�к�ɽ��2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪��P�������ǣ�2����3������ô��P����ԭ��ĶԳƵ�P1��������_____��
��2����3�� ������������������ߵ�P�������ǣ�2����3���� ���P����ԭ��ĶԳƵ�P1�������ǣ���2��3���� �ʴ�Ϊ������2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�к�ɽ��2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��������y=2��x+1��2��2��ͼ��������ƽ��1����λ���ȣ�������ƽ��3����λ���ȣ�������Ϊ��������
A. ����2��1�� B. ��2��1�� C. ��0��1�� D. ����2����5��
A �����������������y=2��x+1��2��2��ͼ��������ƽ��1����λ���ȣ�������ƽ��3����λ���ȣ��� y=2��x+2��2+1�� ��������Ϊ����2��1���� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ���������2017-2018ѧ��ȵ�һѧ����ĩ��ѧ�Ծ����� ���ͣ������
���ʵ��a��b���㣨a-3��2+|b+1|=0����ô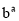 = ��
= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018��2017��������ĩ��̾� ���ͣ������
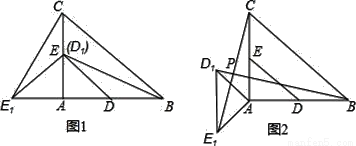
��Rt��ABC�У���A=90�㣬AC=AB=4��D��E�ֱ��DZ�AB��AC���е㣬������Rt��ADE�Ƶ�A��ʱ����ת���õ�����Rt��AD1E1������ת��Ϊ����0������180�㣩����ֱ��BD1��CE1�Ľ���ΪP��
��1����ͼ1������=90��ʱ���߶�BD1�ij��������������������߶�CE1�ij���������������������ֱ����д�����
��2����ͼ2������=135��ʱ����֤��BD1=CE1����BD1��CE1.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com