
如图,在铁路旁有一李庄O,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
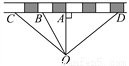
A. A点 B. B点 C. C点 D. D点
A 【解析】试题解析:根据垂线段最短可得:应建在A处, 故选A.科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:解答题
若将一个自然数各位上的数字按照从高位数字到低位数字排成一列后,后一个人数减去前一个数的差是一个常数,则这个数叫做“幸福数”.如:四位数2468排成一列后为:2,4,6,8.因为8-6=6-4=4-2=2,且差为2的常数,故2468是一个差为2的四位“幸福数”.又如,9876,6666等也是“幸福数”.
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同,则称这两个数为“三生三世数”.例如:3579与9753,8765与5678,...,都是“三生三世数”.
规定:把高位数字为x,差为2的三位“幸福数”与它的“三生三世数”的和与222的商记为F(x).例如当x=5时,三位“幸福数”为579,它的“三生三世数”为975,三位“幸福数”与它的“三生三世数”的和为:579+975=1554,1554÷222=7,所以F(x)=7.
(1)计算:F(1), F(4);
(2)已知F(x) =4,求x的值.
(1)F(1) =3,F(4) =6;(2) x=2. 【解析】试题分析:(1)根据题意可得“幸福数”与“三生三世数”,然后按所规定的运算顺序进行计算即可得; (2)设三位数的最高位为x,根据定义表示出“幸福数”与“三生三世数”,然后按规定的运算顺序列出方程,解方程即可得. 试题解析:(1)由题可知, 当x=1时,“幸福数”:135;“三生三世数”:531 F(1)=...查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:单选题
某广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3 m,此时距喷水管的水平距离为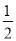 m,在如图的平面直角坐标系中,这个喷泉的函数表达式是( )
m,在如图的平面直角坐标系中,这个喷泉的函数表达式是( )
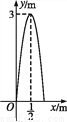
A. y=-3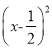 +3 B. y=-3
+3 B. y=-3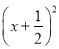 +3 C. y=-12
+3 C. y=-12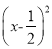 +3 D. y=-12
+3 D. y=-12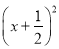 +3
+3
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:填空题
不等式组 的整数解是______.
的整数解是______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:单选题
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数是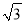 和-1,则点C所对应的实数是( )
和-1,则点C所对应的实数是( )

A. 1+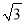 B. 2+
B. 2+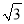 C. 2
C. 2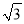 -1 D. 2
-1 D. 2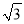 +1
+1
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:解答题
为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
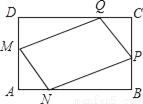
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:填空题
直线y=m是平行于X轴的直线,将抛物线y=-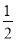 x2-4x在直线y=m上侧的部分沿直线 y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图像,若新的函数图像刚好与 直线y=-x有3个交点,则满足条件的m 的值为_________
x2-4x在直线y=m上侧的部分沿直线 y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图像,若新的函数图像刚好与 直线y=-x有3个交点,则满足条件的m 的值为_________
查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型:解答题
如图,B是线段AD上一动点,沿A至D的方向以2cm/s的速度运动,C是线段BD的中点,AD=10cm.设点B运动的时间为t s.
(1)当t=2 s时,①AB= cm;
②求线段CD的长度.

(2)在运动过程中,若线段AB的中点为E,则EC的长是否变化?若不变。求出EC的长;若发生变化,请说明理由。
(1)①A=4cm ; ②CD=3cm;(2)不变,EC=5cm,理由详见解析. 【解析】试题分析:(1)①根据AB=2t即可得出结论;②先求出BD的长,再根据C是线段BD的中点即可得出CD的长; (2)直接根据中点公式即可得出结论. 试题解析:【解析】 (1)①∵B是线段AD上一动点,沿A至D以2cm/s的速度运动,∴当t=2时,AB=2×2=4cm. ②∵AD=10c...查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:填空题
若正方形的边长为6cm,则其外接圆半径是___________;
3cm 【解析】如图所示:作OE⊥BC, ∵四边形ABCD是O的内接正方形, ∴∠OBE=45°,而OE⊥BC, ∴BE=CE, ∴EB=OE=3, ∴BO=3. 故其半径等于3. 故答案为:3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com