
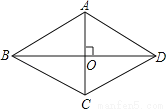
如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件_______,使ABCD成为菱形(只需添加一个即可)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:单选题
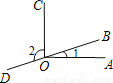
如图,点B,O,D在同一直线上,若∠1=15°,∠2=105°,则∠AOC的度数是( )
A. 75° B. 90° C. 105° D. 125°
B. 【解析】 试题分析:∵∠2=105°,∴∠BOC=180°-∠2=75°,∴∠AOC=∠1+∠BOC=15°+75°=90°. 故选B.查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
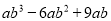 .
.
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
下列各式从左到右的变形中,是因式分解的为( )
A. 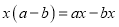 B.
B. 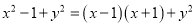
C. 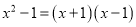 D.
D. 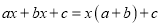
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:解答题
如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.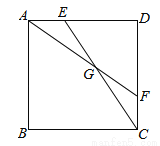
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
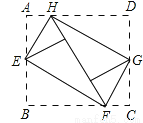
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
C 【解析】∵∠1=∠2,∠3=∠4, ∴∠2+∠3=90°, ∴∠HEF=90°, 同理四边形EFGH的其它内角都是90°, ∴四边形EFGH是矩形. ∴EH=FG(矩形的对边相等); 又∵∠1+∠4=90°,∠4+∠5=90°, ∴∠1=∠5(等量代换), 同理∠5=∠7=∠8, ∴∠1=∠8, ∴Rt△AHE≌Rt△CFG, ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
下列各命题的逆命题成立的是( )
A. 全等三角形的对应角相等 B. 如果两个数相等,那么它们的绝对值相等
C. 两直线平行,同位角相等 D. 如果两个角都是45°,那么这两个角相等
C 【解析】试题分析:首先写出各个命题的逆命题,再进一步判断真假. 【解析】 A、逆命题是三个角对应相等的两个三角形全等,错误; B、绝对值相等的两个数相等,错误; C、同位角相等,两条直线平行,正确; D、相等的两个角都是45°,错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:单选题
如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③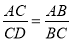 ;④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
;④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
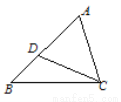
A. 1 B. 2 C. 3 D. 4
C 【解析】【解析】 有三个. ①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定; ②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定; ③中∠A不是已知的比例线段的夹角,不正确; ④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定; 故选C.查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:填空题
当x_________时分式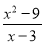 的值为0
的值为0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com